1. találat: Kavics Kupa 2019 1. feladat
Témakör: *Kombinatorika (geometria) (Azonosító: kk_2019_01f )
Sagres városában Tengerész Henrik navigációs iskolát alapított. Ennek kapuja felett a következő díszítés volt látható:
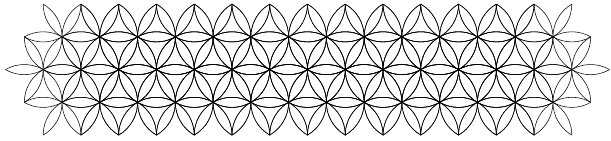
Legalább hányszor kell leszúrni a körzőt ahhoz, hogy ezt az ábrát megrajzolhassuk?
*Kombinatorika (Azonosító: kk_2019_02f )
A sagres-i iskolához csillagvizsgáló is tartozott. Az itt dolgozó csillagász katalógust készített a tengeri tájékozódásban használható csillagokról. Minden ilyen csillagnak egy olyan kilencjegyű azonosító számot adott, melyben minden előforduló számjegy pontosan annyiszor szerepel, mint amennyi a számjegy értéke (pl. az egyik csillag száma: 313553555). Legfeljebb hány csillag kaphatott ilyen azonosító-számot?
*Geometria (Azonosító: kk_2019_03f )
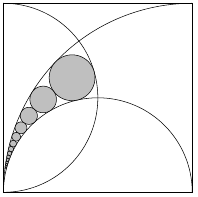
A sagres-i iskolában úgy tartották, hogy csak abból válhat biztos kezű térképrajzoló, aki nagy méretben is pontosan meg tudja szerkeszteni az itt látható ábrát. Ebben két félkört és egy negyedkört szerkesztettek egy négyzetbe, majd az egyik keletkező síkrészbe egyre kisebb szürke köröket szerkesztettek úgy, hogy sorra érintsék egymást és a térrészt határoló nagyobb köríveket is. Nektek nem muszáj megszerkesztenetek az ábrát. Elég, ha megmondjátok, hogy a szürke körök közül a tizedik legnagyobbnak a sugara hányad része a négyzet oldalának. A megoldás egy tört, a válasz a tört legegyszerűbb alakjában a számláló és a nevező összege!
*Algebra (Azonosító: kk_2019_04f )
A tengerészeti iskola hullámtani kurzusának legkönnyebb elméleti feladatai közé tartozott a következő: Hány olyan $ 0 \le x < 2\pi $ valós szám van, amelyre teljesül a $ \sin x + \cos^2 x + \sin^3 x + \cos^4 x = 2 $ egyenlet?
*Geometria (Azonosító: kk_2019_05f )
A sagres-i iskola vitorlatervezési tanszékéről származik ez és a következő feladat. Az $ ABC $ háromszög szimmetrikus az $ AD $ magasságvonalára. A $ B $ csúcs belső szögfelezője az $ AC $ oldalt $ E $ pontban metszi. Az $ ADC $ háromszög beírt körének középponjta $ K $. Tudjuk, hogy $ BEK\sphericalangle = 45^\circ $ . Hány fokos lehet a $ BAC\sphericalangle $? A válasz az összes lehetséges érték összege.
*Geometria (Azonosító: kk_2019_06f )
Az $ ABCD $konvex négyszögben $ BC = 3 $, $ CD = 5 $, $ BCD\sphericalangle = 120^\circ $ . Legyen $ E $, $ F $ és $ G $ rendre az $ ABC $, $ BCD $ és $ ACD $ háromszögek súlypontja. Mekkora az $ ABCD $ négyszög területének a négyzete, ha tudjuk, hogy $ EFG $ háromszög szabályos?
*Algebra (Azonosító: kk_2019_07f )
Mielőtt belevetette magát a gömbi geometria alapos tanulmányozásába, Kolumbusz Kristóf a $ \pi $-vel való számolást gyakorolta. Először felírta a füzetébe a $ \pi $-t (nem tizedestört alakban, hanem a görög betűvel). Ezután felírt a füzetébe még újabb számokat is, a következő szabályok szerint:
(1) Ha egy szám már szerepelt a füzetben, akkor felírhatta a kétszeresét, az ellentettjét és a reciprokát.
(2) Ha két szám szerepelt a füzetben, akkor felírhatta az összegüket is.
(3) Ha egy szám már szerepel, azt másféle alakjába is átírhatta, így például ha $ \dfrac{1}{ \pi+\dfrac 1 \pi} $ már szerepelt, akkor felírhatta ezt is: $ \dfrac{\pi}{ \pi^2+1} $ ; hiszen $ \dfrac{1}{ \pi+\dfrac {1} \pi}=\dfrac{1}{\dfrac{\pi^2+1}{\pi}}=\dfrac{\pi}{ \pi^2+1} $.
A $ \pi^2;\ \pi^3;\ \pi^4;\ \ldots;\ \pi^{1492}$ számok közül legfeljebb hányat írhatott fel a füzetébe?
*Algebra (Azonosító: kk_2019_08f )
Az Atlanti-óceán időjárásának előrejelzéséhez Kolumbusz megkereste a legkisebb fokú egész együtthatós primitív polinomot, amelynek $ \cos 18^\circ $ gyöke. A válasz ezen polinom együtthatóinak abszolútértékeinek összege. Egy egész együtthatós polinom primitív, ha együtthatóinak legnagyobb közös osztója 1.
*Algebra (Azonosító: kk_2019_09f )
Kolumbusz Kristóf sokáig nem tudta, hány matrózt fog tudni összeszedni első útjára. Mindenesetre egyenlő bért akart nekik fizetni, ezért olyan számokat gyűjtött, amelyeket sokféleképpen lehet egyenlően szétosztani. Így a füzetébe összeírta az összes olyan $ 1 $-nél nagyobb de $ 1492 $-nél kisebb pozitív egész számot, amelyre teljesül, hogy több osztója van, mint az összes nála kisebb pozitív egész számnak. Hány számot gyűjtött össze?
*Algebra (Azonosító: kk_2019_10f )
A Pinta kapitánya, Martin Alonso Pinzon a következo parancsot adta a matrózoknak: készítsenek egy színes zászlót, a következo eloírások szerint: a zászló legyen négyzet alakú, mely $ 4 \times 4 $ kisebb négyzet alakú mezore van felosztva. Minden kis négyzet legyen kifestve valamilyen színure úgy, hogy a zászló minden $ 2 \times 2 $ résznégyzetében legyen két egyforma színu négyzet. Legfeljebb hány különbözo szín szerepelhet a zászlón?
*Geometria (Azonosító: kk_2019_11f )
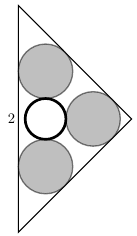
Három hordó bort és egy hordó vizet szeretnénk elhelyezni egy hajó tatjában kialakított tárolóhelyen. Mindegyik hordó 1 egység magas, egyenes henger alakú. A három boroshordó egyforma keresztmetszetu, a vizeshordó lehet náluk kisebb vagy nagyobb. Az alábbi felülnézeti rajzon látható módon szeretnénk oket elhelyezni: a három egybevágó szürke kör a boroshordókat, a fehér kör a vizeshordót jelöli. A rendelkezésre álló hely felülnézetbol egy 2 egység átfogójú, egyenlo szárú derékszögu háromszög. A boroshordóknak két-két falhoz, a vizeshordónak a három boroshordó közé kell szorulnia. Számítsuk ki, hogy ezen feltételek mellett hány köbegység a négy hordó össztérfogatának legkisebb lehetséges értéke.
*Kombinatorika (Azonosító: kk_2019_12f )
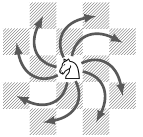
Kolumbusz legénységének egyik tagja jó sakkozó hírében állt. Mivel méltó ellenfelet nem talált a hajón, így inkább a következo feladványon gondolkodott: Egy huszárt elhelyezünk egy mind a négy irányban végtelen sakktábla egy mezojén. Jelölje $ f(n) $, hogy legfeljebb $ n $ lépéssel hány mezot érhet el (például $ f(1) = 9 $, ahogy az ábrán is látható). Léteznek olyan $ a $; $ b $; $ c $ egész számok, amelyekre teljesül, hogy ha $ n $ elég nagy, akkor $ f(n) = an^2 + bn + c $. Határozd meg az $ \left|a \right|\cdot \left|b \right| \cdot \left| c\right|$ szorzat értékét.
*Algebra (Azonosító: kk_2019_13f )
Kolumbusz expedíciója Hispaniola szigetén különös szépségu drágakore lelt. A drágako egy olyan konvex poliéder, amelynek hat egybevágó négyzetlapja és nyolc egybevágó szabályos hatszöglapja van. A négyzetlapok területe egyenként 8 négyzethüvelyk, és közülük semelyik kettonek nincs közös csúcsa. Hány köbhüvelyk a drágako térfogata?
*Algebra (Azonosító: kk_2019_14f )
Egy szigeten élo indiánok egy a tízestől különböző számrendszerben számolnak. Egy tengerész észrevette, hogy ebben a számrendszerben a kilences és a négyes oszthatóság szabálya éppen fordítva van, mint a tízes számrendszerben. Tehát egy szám pontosan akkor osztható 4-gyel, ha a számjegyeinek összege osztható 4-gyel; és pontosan akkor osztható 9-cel, ha az utolsó két számjegye által alkotott szám osztható 9-cel (de ha csak az utolsó számjegyet ismerjük, az még nem elég a 9-cel való oszthatóság eldöntéséhez). A tengerész azt is megállapította, hogy az indiánok számrendeszerének alapja a legkisebb olyan szám, amelyre ez teljesül. Mi az indiánok számrendeszerének alapja?
*Algebra (Azonosító: kk_2019_15f )
1500 tavaszán egy öt hajóból álló spanyol expedíció újabb területeket fedezett fel Dél-Amerika partjainál, ahol mesés gazdagságot ígéro zsákmányra leltek. Öt új telepet is létrehoztak, ezeket sorban I., II., III., IV. és V. Ferdinánd kasztíliai királyokról nevezték el. Osszel aztán mindegyik telepről indulva hazatért egy-egy hajó, rakománnyal gazdagon megpakolva. A visszatért hajók a mesebeli gazdagság hírét messzire terjesztették: így az $ N $ Ferdinánd teleprol visszatéro hajó helyett a következo tavasszal már egy $ N $ hajóból álló flotta indult Amerika felé: az $ N $ hajó közül egy az I. Ferdinánd telepre, egy a II. Ferdinánd telepre stb... végül az $ N. $ az $ N. $ Ferdinánd telepre tartott. Ősszel aztán mindegyik hajó visszatért, és az elozo évhez hasonlóan terjeszetette tovább a mesés gazdagság hírét (tehát ha egy őszön $ k $ db hajó érkezett haza az $ N. $ Ferdinánd teleprol, ezek helyett összesen $ k\cdot N $ hajó indult útnak a következo tavasszal). Ez így folytatódott a következo évtizedben. Az 1510 oszén visszatéro hajóknak hányad része érkezik a II. Ferdinánd teleprol? A válasz a kapott tört legegyszerubb alakjában a számláló és a nevezo összege.
*Algebra (Azonosító: kk_2019_16f )
Santo Domingo egyik kocsmájában kilenc matróz felírta a falra, hogy hány napja nem jártak Európában. A következo számok kerültek a falra: 256, 384, 448, 480, 496, 504, 508, 510 és 511. Melyik az a legnagyobb pozitív egész szám, amely nem állítható elő a falon szereplő számok összegeként? (Többször is felhasználhatjuk ugyanazt a számot az összeg képzésénél.)
*Algebra (Azonosító: kk_2019_17f )
Egy karakk és egy karavella néhány óra különbséggel indult el ellenkezo útvonalon: a karakk Arboletes kikötojébol az onnan 330 tengeri mérföld távolságban levo Barahona kikötojébe tartott, míg a karavella Barahonából Arboletesbe. A két hajó egyszerre ért a közbeeso Cartagena kikötohöz, idáig a karavella átlagsebessége éppen másfél csomóval volt nagyobb a karakkénál (1 csomó sebesség éppen 1 tengeri mérföld óránként). Cartagenára éppen vihar csapott le, ezért mindkét hajó 20 órát vesztegelt ebben a kikötoben. Ennek elmúltával egybol továbbindultak, és innentol olyan jó oldalszéllel haladtak, hogy mindkét hajó átlagsebessége negyedével nagyobb volt a megállás utáni szakaszon, mint a megállás elotti szakaszon. Így végül a karakk 8 órával, míg a karavella 16 órával késobb ért el céljához, mint ha megállás nélkül, az eredeti átlagsebességgel haladtak volna. Hány tengeri mérföldre van Cartagena kikötoje Arboletes kikötojétol?
*Algebra (Azonosító: kk_2019_18f )
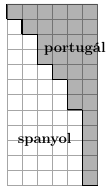
tordesillasi szerzodés felosztotta az Újvilágot Spanyolország és Portugália között. Két értékes sziget azonban éppen ráesik a nyugati 48-adik hosszúsági körre, így ezekrol külön kell rendelkeznie VI. Sándor pápának. Az elso kérdéses sziget téglalap alakú és 72 négyzet alakú parcellára tagolódik, az ábrán látható módon. A pápa úgy szeretné felosztani a szigetet a portugál és a spanyol uralkodó között, hogy ha egy parcella a portugáloknak jut, akkor minden attól keletre vagy északra levo parcella is a portugálok kezére kerüljön. Emellett azt is szeretné, hogy a portugál parcellák száma 3-mal osztva 1 maradékot adjon. Hány olyan felosztás van, amely mindegyik elvárást kielégíti? Az ábrán egy lehetséges felosztás látható, a portugálok részét szürkével jelöltük.
*Algebra (Azonosító: kk_2019_19f )
A másik kérdéses sziget kör alakú. Ennek partján tíz kikötofalu, míg a belsejében öt további település található. A pápának most ezt a 15 települést kell szétosztania a portugálok és a spanyolok között úgy, hogy a szétosztás után mindkét ország létrehozhasson egy összefüggo szárazföldi úthálózatot a saját városai között, a következo kívánalmak szerint:
1. Portugál út ne menjen be spanyol városba és spanyol út se menjen portugál városba.
2. Portugál út sehol ne keresztezzen spanyol utat.
Hány olyen szétosztás van, amely megfelel ennek a feltételnek? (Az is lehet, hogy az összes települést egy ország kapja).
*Algebra (Azonosító: kk_2019_20f )
Magellán utazása tervezéséhez egy földgömböt készített. Ezen különbözo színekkel bejelölt 15 kikötot, ahol már járt életében. Egy-egy kikötovel megegyezo színnel megjelölte a földgömb átellenes pontját is. Ezután minden színhez feldobott egy pénzt, és ennek eredménye alapján a két egyforma színu pötty egyikét letörölte. Így megint 15 különbözo színu pontja maradt. Számítsuk ki annak a valószínuségét, hogy ennek a 15 pontnak a konvex burka nem tartalmazza a földgömb középpontját. A válasz a kapott tört legegyszerubb alakjában a számláló és a nevezo összege.


