Egy téglalapot hat tartományra osztottak fel az ábrán látható módon.

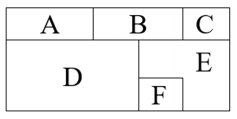Az $ A $, $ B $, $ C $, $ D $, $ E $, $ F $ tartományokat úgy kell kiszínezni, hogy azonos színű tartományok ne érintkezzenek egymással. A színezéshez a piros, kék, zöld és sárga színek használhatók. (Mindegyik tartományt ki kell színezni a megadott színek egyikével, de nem kötelező mind a négy színt felhasználni.)

a) Hányféleképpen színezhető ki a téglalap úgy, hogy az $ A $ és $ C $ tartományok színe különböző legyen?

Az $ A $, $ B $, $ C $, $ D $, $ E $ és $ F $ nemnegatív számokról a következőket tudjuk:

(1) A = 6 és D = 8;

(2) B számtani közepe A-nak és C-nek;

(3) F mértani közepe D-nek és E-nek;

(4) F 1-gyel nagyobb B-nél;

(5) E 2-vel nagyobb C-nél.

b) Határozza meg az ismeretlen számok értékét!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Egy ingatlanhirdetésben sík területen fekvő legelőt kínálnak eladásra. A legelő alakja konvex négyszög, ennek csúcsait jelölje $ A $, $ B $, $ C $ és $ D $. A négyszög három oldala $ AB = 126\,m $, $ BC = 65\,m $, $ CD = 80\,m $, két szöge $ ABC\sphericalangle = 122,5^\circ $ és $ ADC\sphericalangle = 90^\circ $. A legelőt $ 0,9 $ hektár területűnek hirdeti az eladó.

a) Hány százalékkal nagyobb a legelő valódi területe a meghirdetettnél? ($ 1\,ha = 10\,000\,m^2 $)

Egy itatóvályú alakja háromszög alapú egyenes hasáb. Vízszintes helyzetében a vályú felül nyitott, a hasábnak ez a lapja párhuzamos a vízszintes talaj síkjával, a háromszög alakú lapok pedig a talaj síkjára merőlegesek.

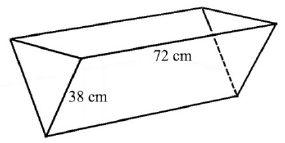
A szabályos háromszög alakú lemezek oldalai 38 cm hosszúak, a két téglalap alakú oldallap pedig 38 cm × 72 cm-es.

A vízszintes helyzetű vályú kezdetben tele van vízzel. A vályú egyik végét megemeljük, ezért a víz egy része kifolyik belőle.

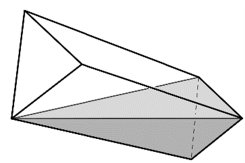A vályúban ekkor a vízfelszín a bal oldali szabályos háromszög alsó csúcsától a jobb oldali szabályos háromszög felső éléig ér, ahogyan az ábra mutatja.

b) Igazolja, hogy ekkor a vályúban (egészre kerekítve) 15 liter víz van!

A vályút ezután visszafektetjük eredeti, vízszintes helyzetébe.

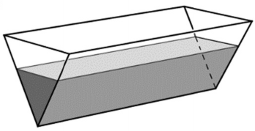c) Hány cm magasan áll a víz a vályúban ekkor?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

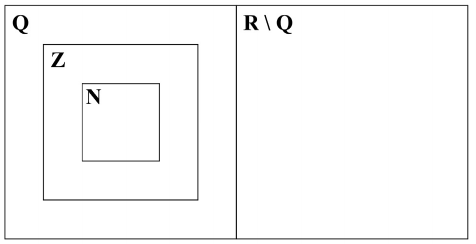
a) Az $ f $  függvény hozzárendelési szabálya $ f(x) = 3^{-x}$ ($ x \in\mathbb{R} $). Helyezze el az alábbi halmazábra megfelelő részeibe az $ f (-2) $, $ f (0,5) $ és $ f (5) $ függvényértékeket!

Egy ötpontú egyszerű gráf $ A $, $ B $, $ C $, $ D $, $ E $ pontjaihoz rendre a $ 3^{-2} $, $ 3^{-7} $, $ 3^{-12} $, $ 1- \sqrt{ 2 } $ és $ \dfrac{1}{\sqrt{ 2 } - 1} $ számokat írtuk. A gráfban két pont akkor és csak akkor van éllel összekötve, ha a két ponthoz írt számok összege racionális szám.

b) Hány éle van ennek az ötpontú gráfnak?

A koordinátatengelyek és a $ g( x ) = 3^{- x} $ ($ x \ge 0 $) függvény grafikonja által határolt tartományba olyan egymáshoz csatlakozó téglalapokat írunk, amelyek egyik oldala az x-tengelyen van és egységnyi hosszúságú, egyik csúcsa pedig a $ g $ függvény grafikonjára illeszkedik.

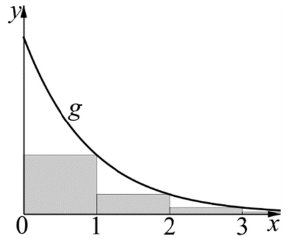Az első beírt téglalap egyik csúcsa az origó, ezzel szemközti csúcsa pedig az $ (1; g(1)) $ pont. A további téglalapok egy-egy csúcsa rendre $ (2; g(2)) $, $ (3; g(3)) $, és így tovább, az ábra szerint (az ábra nem méretarányos). Legyen $ n $ az a legnagyobb pozitív egész szám, amelyre $ g(n) - g(n + 1) > 10^{- 6} $ teljesül.

c) Számítsa ki az első $ n $ téglalap területének összegét!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Egy téglatest egyik éle $ 4\,dm $, egy másik éle $ 2\,dm $ hosszú. A téglatest térfogata $ 72\,dm^3 $.

a) Határozza meg a téglatest felszínét!

Egy téglatest térfogata $ 72\,dm^3 $. A téglatest egyik éle kétszer olyan hosszú, mint egy másik éle.

b) Határozza meg az ilyen tulajdonságú téglatestek közül a minimális felszínű téglatest éleinek hosszát!

c) Hányféleképpen választhatunk ki egy téglatest csúcsai közül hármat úgy, hogy a kiválasztott három csúcs által meghatározott sík ne tartalmazza a téglatest egyetlen további csúcsát sem?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Egy jótékonysági rendezvényen sorsjegyeket árulnak. 5 kék és 3 zöld sorsjegy 6700 Ft-ba, 3 kék és 2 zöld sorsjegy 4200 Ft-ba kerül.

a) Mennyibe kerül külön-külön egy kék, illetve egy zöld sorsjegy?

A sorsjegyek $ 40\% $-a kék, $ 60\% $-a zöld. A különböző színű sorsjegyekhez tartozó nyeremények arányát mutatja a táblázat (például az összes kék sorsjegynek a $ 35\% $-a tárgynyereményt nyer).

Véletlenszerűen kiválasztunk egy sorsjegyet. Legyen az $ A $ esemény az, hogy ez a sorsjegy tárgynyereményt nyer, a $ B $ esemény pedig az, hogy ez a sorsjegy kék.

b) Igazolja, hogy $ P(A) = 0,38 $. Számítsa ki a $ P(B | A) $ feltételes valószínűséget! Függetlenek-e az A és B események?

c) Határozza meg az egy kék sorsjegyre eső nyeremény várható értékét, ha a tárgynyereményt 500 Ft-os értéken vesszük figyelembe!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba