a) Az $ f $  függvény hozzárendelési szabálya $ f(x) = 3^{-x}$ ($ x \in\mathbb{R} $). Helyezze el az alábbi halmazábra megfelelő részeibe az $ f (-2) $, $ f (0,5) $ és $ f (5) $ függvényértékeket!

Egy ötpontú egyszerű gráf $ A $, $ B $, $ C $, $ D $, $ E $ pontjaihoz rendre a $ 3^{-2} $, $ 3^{-7} $, $ 3^{-12} $, $ 1- \sqrt{ 2 } $ és $ \dfrac{1}{\sqrt{ 2 } - 1} $ számokat írtuk. A gráfban két pont akkor és csak akkor van éllel összekötve, ha a két ponthoz írt számok összege racionális szám.

b) Hány éle van ennek az ötpontú gráfnak?

A koordinátatengelyek és a $ g( x ) = 3^{- x} $ ($ x \ge 0 $) függvény grafikonja által határolt tartományba olyan egymáshoz csatlakozó téglalapokat írunk, amelyek egyik oldala az x-tengelyen van és egységnyi hosszúságú, egyik csúcsa pedig a $ g $ függvény grafikonjára illeszkedik.

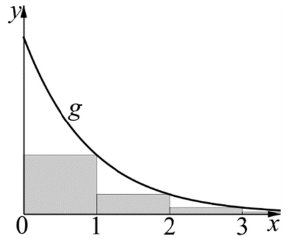Az első beírt téglalap egyik csúcsa az origó, ezzel szemközti csúcsa pedig az $ (1; g(1)) $ pont. A további téglalapok egy-egy csúcsa rendre $ (2; g(2)) $, $ (3; g(3)) $, és így tovább, az ábra szerint (az ábra nem méretarányos). Legyen $ n $ az a legnagyobb pozitív egész szám, amelyre $ g(n) - g(n + 1) > 10^{- 6} $ teljesül.

c) Számítsa ki az első $ n $ téglalap területének összegét!

Megoldás:

a) Beírhatók jól az ábrába

b) 4 él

c) $ \dfrac{1}{3}\cdot \dfrac{\left(\dfrac{1}{3}\right)^{12}-1 }{\dfrac{1}{3}-1}\approx 0,5 $