Egy ingatlanhirdetésben sík területen fekvő legelőt kínálnak eladásra. A legelő alakja konvex négyszög, ennek csúcsait jelölje $ A $, $ B $, $ C $ és $ D $. A négyszög három oldala $ AB = 126\,m $, $ BC = 65\,m $, $ CD = 80\,m $, két szöge $ ABC\sphericalangle = 122,5^\circ $ és $ ADC\sphericalangle = 90^\circ $. A legelőt $ 0,9 $ hektár területűnek hirdeti az eladó.

a) Hány százalékkal nagyobb a legelő valódi területe a meghirdetettnél? ($ 1\,ha = 10\,000\,m^2 $)

Egy itatóvályú alakja háromszög alapú egyenes hasáb. Vízszintes helyzetében a vályú felül nyitott, a hasábnak ez a lapja párhuzamos a vízszintes talaj síkjával, a háromszög alakú lapok pedig a talaj síkjára merőlegesek.

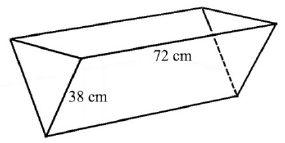
A szabályos háromszög alakú lemezek oldalai 38 cm hosszúak, a két téglalap alakú oldallap pedig 38 cm × 72 cm-es.

A vízszintes helyzetű vályú kezdetben tele van vízzel. A vályú egyik végét megemeljük, ezért a víz egy része kifolyik belőle.

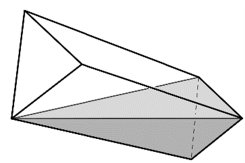A vályúban ekkor a vízfelszín a bal oldali szabályos háromszög alsó csúcsától a jobb oldali szabályos háromszög felső éléig ér, ahogyan az ábra mutatja.

b) Igazolja, hogy ekkor a vályúban (egészre kerekítve) 15 liter víz van!

A vályút ezután visszafektetjük eredeti, vízszintes helyzetébe.

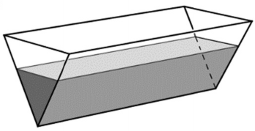c) Hány cm magasan áll a víz a vályúban ekkor?

Megoldás:

a) $ \approx 5\% $

b) Igaz az állítás

c) $ \approx 19\,cm $