a) Igazolja, hogy a $\left(-\dfrac 1 2\right) $, a $ 0 $ és a $ 3 $ is gyöke a $ 2 x ^3- 5 x^2 - 3 x = 0 $ egyenletnek,és az egyenletnek ezeken kívül más valós gyöke nincs!

b) Oldja meg az alábbi egyenletet a valós számok halmazán! $ 2 \cos^3 x - 5 \cos^2 x - 3 cos x = 0 $

c) Mutassa meg, hogy a $ 2 \cdot 8^x + 7 \cdot 4^x + 3 \cdot 2^x = 0 $ egyenletnek nincs valós gyöke!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Egy üzemben olyan digitális műszert gyártanak, amely kétféle adat mérésére alkalmas: távolságot és szöget lehet vele meghatározni. A gyártósor meghibásodott, de ezt hosszabb ideig nem vették észre. Ezalatt sok mérőeszközt gyártottak, ám ezeknek csak a $ 93\% $-a adja meg hibátlanul a szöget, a $ 95\% $-a méri hibátlanul a távolságot, sőt a gyártott mérőeszközök $ 2\% $-a mindkét adatot hibásan határozza meg.

a) Az egyik minőségellenőr 20 darab műszert vizsgál meg visszatevéses mintavétellel a meghibásodási időszak alatt készült termékek közül. Mekkora annak a valószínűsége, hogy legfeljebb 2 darab hibásat talál közöttük? (Egy műszert hibásnak tekintünk, ha akár a szöget, akár a távolságot hibásan méri.)

Vízszintes, sík terepen futó patak túlpartján álló fa magasságát kell meghatároznunk. A síkra merőlegesen álló fát megközelíteni nem tudjuk, de van egy kisméretű, digitális műszerünk, amellyel szöget és távolságot is pontosan tudunk mérni. A patakparton kitűzzük az $ A $ és $ B $ pontokat, amelyek 10 méterre vannak egymástól. Az $ A $ pontból $ 55^\circ $-os, a $ B $-ből $ 60^\circ $-os emelkedési szög alatt látszik a fa teteje. Szögméréssel még megállapítjuk, hogy $ ATB \angle = 90^\circ $ , ahol $ T $ a fa "talppontja".

b) Milyen magas a fa?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Egy növekvő számtani sorozat első három tagjából álló adathalmaz szórásnégyzete 6.

a) Igazolja, hogy a sorozat differenciája 3-mal egyenlő!

András, Barbara, Cili, Dezső és Edit rokonok. Cili 3 évvel idősebb Barbaránál, Dezső 6 évvel fiatalabb Barbaránál, Edit pedig 9 évvel idősebb Cilinél. Dezső, Barbara és Edit életkora (ebben a sorrendben) egy mértani sorozat három egymást követő tagja, András, Barbara és Cili életkora (ebben a sorrendben) egy számtani sorozat három szomszédos tagja.

b) Hány éves András?

András, Barbara, Cili, Dezső, Edit és Feri moziba mennek.

c) Hányféleképpen foglalhatnak helyet hat egymás melletti széken úgy, hogy a három lány ne három egymás melletti széken üljön?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Egy $ ABCD $ négyzet $ A $ csúcsa a koordinátarendszer $ y $ tengelyére, szomszédos $ B $ csúcsa pedig a koordinátarendszer $ x $ tengelyére illeszkedik.

a) Bizonyítsa be, hogy a négyzet $ K $ középpontjának koordinátái vagy egyenlők, vagy egymás ellentettjei!

b) Egy ilyen négyzet középpontja a $ (7; 7) $ pont. A négyzet oldala 10 egység hosszú. Számítsa ki a négyzet koordinátatengelyekre illeszkedő két csúcsának koordinátáit!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Kovács úr a tetőterébe egy téglatest alakú beépített szekrényt készíttet. Két vázlatot rajzolt a terveiről az asztalosnak, és ezeken feltüntette a tetőtér megfelelő adatait is. Az első vázlat "térhatású", a második pedig elölnézetben ábrázolja a szekrényt.

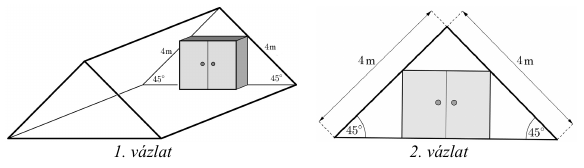
A tetőtér adottságai miatt a szekrény mélységének pontosan $ 60\ cm $-nek kell lennie.

a) Mekkora legyen a szekrény vízszintes és függőleges mérete (azaz a szélessége és a magassága), ha a lehető legnagyobb térfogatú szekrényt szeretné elkészíttetni? (A magasság, a szélesség és a mélység a szekrény külső méretei, Kovács úr ezekkel számítja ki a térfogatot.)

A szekrény elkészült. Az akasztós részébe Kovács úr vasárnap este 7 inget tesz be, a hét minden napjára egyet-egyet. Az ingek között van 2 fehér, 2 világoskék és 3 sárga. Reggelente nagyon siet, ezért Kovács úr csak benyúl a szekrénybe, és anélkül, hogy odanézne, véletlenszerűen kivesz egy inget.

b) Mennyi a valószínűsége annak, hogy a hét első három napján vagy három különböző színű vagy három egyforma színű inget választ? (Ha valamelyik nap viselt egy inget, azt utána már nem teszi vissza a szekrénybe.)

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba