Kovács úr a tetőterébe egy téglatest alakú beépített szekrényt készíttet. Két vázlatot rajzolt a terveiről az asztalosnak, és ezeken feltüntette a tetőtér megfelelő adatait is. Az első vázlat "térhatású", a második pedig elölnézetben ábrázolja a szekrényt.

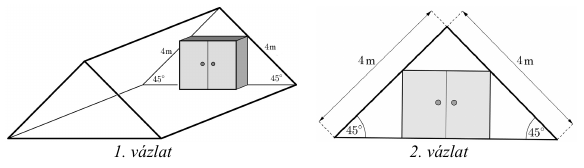
A tetőtér adottságai miatt a szekrény mélységének pontosan $ 60\ cm $-nek kell lennie.

a) Mekkora legyen a szekrény vízszintes és függőleges mérete (azaz a szélessége és a magassága), ha a lehető legnagyobb térfogatú szekrényt szeretné elkészíttetni? (A magasság, a szélesség és a mélység a szekrény külső méretei, Kovács úr ezekkel számítja ki a térfogatot.)

A szekrény elkészült. Az akasztós részébe Kovács úr vasárnap este 7 inget tesz be, a hét minden napjára egyet-egyet. Az ingek között van 2 fehér, 2 világoskék és 3 sárga. Reggelente nagyon siet, ezért Kovács úr csak benyúl a szekrénybe, és anélkül, hogy odanézne, véletlenszerűen kivesz egy inget.

b) Mennyi a valószínűsége annak, hogy a hét első három napján vagy három különböző színű vagy három egyforma színű inget választ? (Ha valamelyik nap viselt egy inget, azt utána már nem teszi vissza a szekrénybe.)

Megoldás:

a) Szélesség: $ \sqrt{2}\approx 1,41$, magassága: $ 2\sqrt{2}\approx 2,83 $

b) $P=\dfrac{13}{35}\approx 0,371$