|
Menü
|
Tengelyes tükrözés
Tukr01
Az AB átmérőjű körvonal egyik félkörívén rögzítsünk egy A-tól és B-től különböző C pontot. A C pontot nem tartalmazó másik féköríven mozgó P pontot tükrözzük az AC illetve a BC egyenesre, a tükörképet jelölje rendre P' és P". Vizsgáljuk meg a P pont különböző helyzetei mellett a P', P" és C pontok kölcsönös helyzetét! Határozzuk meg, hogy mely P pont esetén lesz a P'CP" töröttvonal hossza a lehető legkisebb, illetve a lehető legnagyobb! Határozzuk meg a minimum és a maximum értékét! |
Tukr02
A hegyesszögű ABC háromszög M magasságpontját tükrözzük a háromszög AB, BC, CA oldalegyeneseire, a tükörképek rendre X, Y és Z. - Szerkesszük meg az XYZ háromszög köré írható kört. Mit tapasztalunk? Magyarázzuk meg a látottakat!
- Ha az ABC háromszög megfelelő magasságvonalainak AB, BC és CA oldalain lévő talppontját rendre D, E és F jelöli, akkor számítsuk ki az

összeg értékét! |
Tukr03
A hegyesszögű ABC háromszög magasságpontja M. A BCM, CAM, ABM háromszögek köré írt kör középpontja rendre A', B' és C'. - Keressünk kapcsolatot a BCM, CAM, ABM háromszögek köré írt körök között!
- Milyen kapcsolat van az ABC és az A'B'C' háromszögek között?
- Milyen kapcsolat van az AA', BB' és CC' szakaszok között?
Válaszainkat indokoljuk!
|
Tukr04
Az ABC
hegyesszögű
háromszög egy belső pontja P, a P pont BC,
BA és CA
oldalakra eső merőleges vetülete
rendre A’, C’
és B’. Határozzuk meg
az összes olyan P pontot, amelyre 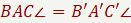 és és  feltételek
teljesülnek! feltételek
teljesülnek! |
|
|