Az ábrán látható számpiramis alsó sorába valamilyen sorrendben az 1, 2, 3, 4, 5 számokat írjuk. Ezután a számpiramis mezőit úgy töltjük ki, hogy minden üres négyzetbe az alatta levő, vele közvetlenül érintkező két négyzetben szereplő szám összege kerüljön. Hányféleképpen lehet kitölteni a számpiramist úgy, hogy a legfelső négyzetben a lehető legnagyobb számot kapjuk?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Egy aula padlója szabályos tízszög alakú. Díszítésként a tízszög minden oldalát és átlóját aranyszínűre festették. Hány olyan derékszögű háromszög keletkezett így, amelynek kerülete aranyszínű és derékszögű csúcsa a szabályos tízszög kerületén van?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Adott az $A = \text{tg } \dfrac{x\cdot \pi}{4}+A \text{tg } \dfrac{y\cdot \pi}{6} $ kifejezés, ahol x és y pozitív egész számok. 

a) Határozza meg az A kifejezés értelmezési tartományát.

b) Amennyiben x és y véletlenszerűen választott, 2022-nél kisebb, különböző pozitív egész számok, akkor adja meg annak valószínűségét, hogy az A kifejezés értelmezhető.

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

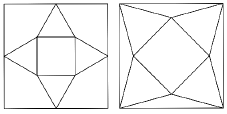
Két egybevágó négyzetbe belerajzoltuk egy-egy négyzet alapú gúla hálóját a mellékelt ábrák szerint. Mindkét gúla rendelkezik azzal a tulajdonsággal, hogy éleinek hossza egyenlő. Mekkora a két gúla térfogatának aránya?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Adja meg a $ p $ pozitív prím paraméter értékét, ha tudjuk, hogy a

$ \dfrac{2}{3} < \dfrac{3p}{5x-2p} < \dfrac{3}{4}  $

egyenlőtlenségrendszernek pontosan egy $ x $ egész megoldása van.

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba