Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium
Látogatók
Összes:
9 198 972
Mai:
5 301
216.73.216.77
(IP: 216.73.216.77)
|
1. találat: OKTV 2015/2016 I. kategória 1. forduló 1. feladat
Témakör: *Kombinatorika (Azonosító: OKTV_20152016_1k1f1f )
A 2015 olyan négyjegyű szám, amelynek számjegyei különbözőek és közülük pontosan kettő prímszám. Hány ilyen négyjegyű természetes szám van?
*Algebra (Azonosító: OKTV_20152016_1k1f2f )
Oldja meg a valós számpárok halmazán az $x+y^2=\dfrac{1}{2},\ x^2+2y=-\dfrac{7}{4}$ egyenletrendszert!
*Geometria (Azonosító: OKTV_20152016_1k1f3f )
A BC átfogójú ABC derékszögű háromszög AB befogójának A pontból induló félegyenesén megjelöljük azt a $B_0$ pontot, amelyre $AB_0=3\cdot AB$ . Azt tapasztaljuk, hogy az $ABC$ és $AB_0C$ háromszögek hasonlók. Bizonyítsa be, hogy az $AB_0C$ háromszögben CB belső szögfelező!
*Algebra (Azonosító: OKTV_20152016_1k1f4f )
Legyenek a $\dfrac{p}{p-2}\cdot x^2+\dfrac{p-1}{p+1}\cdot x+\dfrac{1}{4}=0$ egyenlet valós gyökei $x_1$ és $x_2$. Határozza meg a $p\ne 0$ valós paraméter mindazon értékeit, amelyekre fennáll, hogy $x_1\cdot x_2-(x_1+x_2)=\dfrac{1}{p+1}$
*Algebra (Azonosító: OKTV_20152016_1k1f5f )
Az $a_n$ sorozatra teljesül, hogy $a_1=1$, és minden $n\ge2$ esetén $a_n=\dfrac{a_{n-1}}{2a_{n-1}+1}$. Hány olyan tagja van a sorozatnak, amelyik nagyobb $\dfrac{1}{100}$-nál?
*Geometria (Azonosító: OKTV_20152016_1k1f6f )
A négyzet alakú ABCD asztallapra két egybevágó szabályos háromszöget terítünk le az ábra szerint (a szabályos háromszögek oldalainak hossza egyenlő a négyzet oldalainak hosszával). Határozza meg a kétszer lefedett rész területének és a nem fedett rész területének arányát! 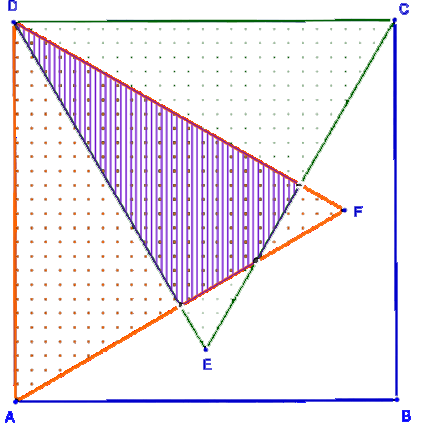
|
|
Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium
|
QR kód
Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium

|
|
Bejelentkezés cikkíróknak
|
|


