a) Oldja meg az alábbi egyenletet a valós számok halmazán!

$ \dfrac{x}{2} + \dfrac{x-1}{3} =8 $

b) Két egymást követő egész szám négyzetének összege 10 513. Melyik ez a két szám?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

A képen látható lépcsőkorlát egy részletének oldalnézete paralelogramma alakú. A paralelogramma függőleges oldalai 80 cm hosszúak, távolságuk 115 cm. A másik két oldal hossza 125 cm. (Az ábra jelöléseit használjuk.)

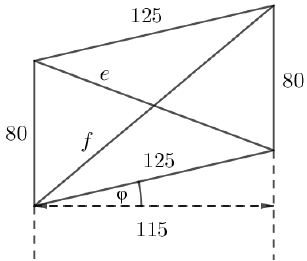
a) A $ \phi $ szög a paralelogramma alsó oldalának a vízszintessel bezárt szöge. Számítással igazolja, hogy (egész fokra kerekítve) $ \phi = 23^\circ $!
b) Számítsa ki a paralelogramma e átlójának hosszát!
c) A lépcsőkorlátra szélfogót szerelnek nádszövetből. Mekkora területű nádszövettel lehet a paralelogramma alakú részt lefedni? Igaz-e, hogy a felszerelt nádszövet területe kisebb $ 1m^2 $-nél?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Most induló kisvállalkozásához András üzleti tervet készít. Tervei szerint az első félévben minden hónapban 300 000 Ft lesz a havi árbevétele. Arra számít, hogy a 7. hónaptól kezdve egészen a második év végéig minden hónapban az előző hónaphoz képest $ 5\% $-os havi árbevétel-növekedést ér majd el.

a) A terv szerint mennyi lesz András havi árbevétele a 24. hónapban, és mennyi összesen a két év alatt? Válaszait tízezer forintra kerekítve adja meg!

András és négy barátja: Balázs, Cili, Dóra és Endre egy ötszemélyes autóval utaznak a Balatonhoz (elöl ketten, hátul hárman ülnek). Jogosítványa csak Andrásnak és Dórának van, így csak ők vezethetik az autót.

b) Hányféle ülésrendben utazhat az autóval az öt fiatal, ha András mindenképpen Cili mellett ül? (Az a két ember, aki elöl ül, egymás mellett ül. Két ülésrend különböző, ha van olyan ember, aki az egyik ülésrendben máshol ül, mint a másikban.)

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Az alábbi táblázatban egy végzős osztály emelt szintű matematikacsoportjának idei próbaérettségi eredményei láthatók. A dolgozattal legfeljebb $ 115 $ pontot lehetett szerezni; $ 60\% $-tól jeles (5), $ 47\% $-tól jó (4), $ 33\% $-tól közepes (3) és $ 25\ % $-tól elégséges (2) osztályzatot lehetett elérni. Az alábbi táblázatba már beírták a szerzett pontszámokat, de a jegyeket még nem mindenkihez.

a) A fenti adatok alapján egészítse ki a táblázatot a hiányzó osztályzatokkal, és készítsen kördiagramot a matematikacsoport osztályzatainak eloszlásáról!

A 33 fős osztály az utolsó tanévben három osztályprogramot szervezett: színházba, moziba, illetve kirándulni mentek. Mindenki részt vett legalább az egyik programon. Színházban és moziban is volt 13 fő, színházban és kirándulni is volt 12 fő, moziban és kirándulni is volt 10 fő. 4 olyan diák volt, aki csak egyetlen programon vett részt.
b) Hányan voltak ott mindhárom osztályprogramon?
A színház 15 soros nézőterén a második sortól kezdve minden sorban ugyanannyival több szék van, mint az előző sorban. A hatodik sorban 26 szék, a tizedik sorban 34 szék van.
c) Hány szék van összesen a nézőtéren?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

A ceruzagyártás folyamatának egyik eleme a ceruzabél készítése. A grafitból, agyagból és koromból álló masszából egy gép először 20 cm átmérőjű, 25 cm magas hengereket présel. A még képlékeny állapotú hengerekből - hulladék keletkezése nélkül - készül a 2 mm átmérőjű hengeres ceruzabélszál.

a) Összesen hány méter hosszú ceruzabélszál készül egy hengerből?

Egy ceruzagyárban jelenleg az ott dolgozó nők és férfiak aránya 3 : 2. Ha felvennének még 5 nőt és 6 férfit, akkor ez az arány 4 : 3-ra módosulna.

b) Hány nő és hány férfi dolgozik jelenleg a gyárban?

Ha egy ceruza leesik az asztalról, akkor 0,2 a valószínűsége annak, hogy kitörik a hegye. Ervin macskája lesodor egy ceruzakészletet az asztalról, így a ceruzák sorban leesnek a földre.

c) Mennyi a valószínűsége annak, hogy a 12 leeső ceruzából legfeljebb egy ceruzának törik ki a hegye?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Az asztalon összesen 36 darab színes papír sokszög van, egy részük háromszög alakú, a többi négyszög alakú. Mindegyik vagy piros, vagy kék színű. 24 sokszög piros, 27 pedig háromszög alakú. Kék négyszögből 5 darab van.

a) Hány piros háromszög van az asztalon?

A 36 sokszögből véletlenszerűen kiválasztunk kettőt (visszatevés nélkül).

b) Mennyi a valószínűsége annak, hogy mindkét választott sokszög háromszög?

Adott egy háromszög három csúcsa a koordinátasíkon: $ A(1; 2) $, $ B(5; 0) $ és $ C(6; 7) $.

c) Igazolja, hogy az $ ABC $ háromszög egyenlő szárú!

d) Határozza meg az $ ABC $ háromszög területét!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba