Egy kisvárosban, ha taxival utazunk, a szolgáltatásért fizetendő viteldíj az alapdíj és a kilométerdíj összege. Az út hosszától független alapdíj 700 Ft, a megtett út hosszával egyenesen arányos kilométerdíj pedig kilométerenként 300 Ft. (A taxióra folyamatosan pörög, nemcsak egész kilométerenként mér.)
a) Hány forint a viteldíj ebben a kisvárosban, ha 12,5 kilométert utazunk taxival?

b) Hány kilométert utaztunk taxival, ha a viteldíj 2275 Ft?
c) Az alábbi koordináta-rendszerben ábrázolja a viteldíjat a megtett út függvényében 0 és 5 kilométer között!

Egy másik kisvárosban a taxis utazás viteldíja szintén alapdíjból és kilométerdíjból tevődik össze. Gergő ebben a városban hétfőn egy 6,5 km hosszú taxizás után 2825 forintot fizetett, kedden pedig egy 10,4 kilométeres út után 4190 forintot.
d) Hány forint ebben a városban az alapdíj, és hány forint a kilométerdíj?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Egy négyzet alapú szabályos gúla alapélének hossza 66 cm, a gúla magassága 56 cm.
a) Számítsa ki a gúla felszínét!
A gúlát két részre vágjuk egy olyan síkkal, amely párhuzamos az alaplappal, és a gúla magasságát felezi.

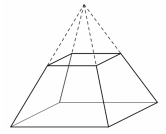b) Számítsa ki az így keletkező csonkagúla térfogatát!
A csonkagúla csúcsait és éleit gráfként is fel tudjuk rajzolni. Az így kapott 8 pontú gráfban minden pont fokszáma 3.

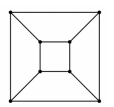c)Létezik-e olyan 7 pontú gráf, amelyben minden pont fokszáma 3? (Ha válasza igen, akkor rajzoljon ilyen gráfot, ha a válasza nem, akkor válaszát indokolja.)

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Dávidnak ebben a félévben három darab 3-as és két darab 5-ös érdemjegye van angolból. Jánosnak is öt jegye van angolból. Az ő jegyeinek mediánja 1-gyel nagyobb, mint Dávid jegyeinek mediánja, az átlaga viszont 1-gyel kisebb Dávid jegyeinek átlagánál.
a) Határozza meg János angoljegyeit! (A jegyek egész számok.)
Eszter az első félévben 9 jegyet szerzett angolból, és ezek átlaga pontosan 3. A második félévben 6 jegyet szerzett, ezek átlaga pontosan 4,5.
b) Mennyi Eszter egész évben szerzett angoljegyeinek az átlaga?
Az $ \left\{ 1; 2; 3; 4; 5 \right\} $ halmaz elemei közül véletlenszerűen kiválasztunk két különbözőt.
c) Mennyi a valószínűsége, hogy a két kiválasztott szám átlaga egész szám lesz?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Egy háromszög csúcsai a koordináta-rendszerben: $ A(5; 6) $, $ B(4; 2) $ és $ C(8; 2) $.
a) Számítsa ki a háromszög $ A $-nál lévő belső szögét!
b) Írja fel a háromszög $ B $-re illeszkedő magasságvonalának egyenletét, és számítsa ki a háromszög $ M $ magasságpontjának koordinátáit!
Az $ ABC $ háromszöget a $ B $ pontból középpontosan a kétszeresére nagyítjuk, így az $ A’B’C’ $ háromszöget kapjuk.
c) Adja meg az $ A’B’C’ $ háromszög csúcsainak koordinátáit!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

a) Egy számtani sorozat második tagja 24, ötödik tagja 81. Hány százalékkal nagyobb a sorozat első 16 tagjának összege a sorozat 106. tagjánál?
b) Egy mértani sorozat második tagja 24, ötödik tagja 81. A sorozat tagjai között hány olyan van, amelyik kisebb, mint 10 000 000?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Egy osztályban kétszer annyian járnak matematikafakultációra, mint fizikafakultációra. Összesen 15 olyan diák van az osztályban, aki a két fakultáció közül valamelyikre jár. A 15 diák közül 6-an mindkét fakultációra járnak.
a) Hány olyan diák van az osztályban, aki matematikafakultációra jár, de fizikára nem?
A távoktatás időszakában ennek az osztálynak a tagjai a tanárral együtt 24-en vesznek részt az alap-matematikaórákon. Az órákon használt online alkalmazás 4 sorban és 6 oszlopban rendezi el a résztvevőket megjelenítő egybevágó kis téglalapokat úgy, hogy ezek kitöltik a teljes képernyőt. Stefi számítógépén a képernyő vízszintes és függőleges oldalának aránya 16 : 9.

b)Adja meg egy kis téglalap vízszintes és függőleges oldalának arányát két egész szám hányadosaként!
Az alkalmazás a bejelentkező személyekhez tartozó 24 téglalapot véletlenszerűen rendezi el a képernyőn. 
c) Számítsa ki annak a valószínűségét, hogy a következő órán Stefit és barátnőjét, Cilit megjelenítő téglalap is a képernyő első sorába fog kerülni! (A 24 kis téglalapot az alkalmazás mindig 4 sorban és 6 oszlopban rendezi el.) 

A 24 bejelentkező személyt a képernyőn 24!-féleképpen lehet elrendezni.
d) Mutassa meg, hogy a 24! osztható 10 000-rel!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba