a) Oldja meg az alábbi egyenletet a valós számok halmazán!

$ ( x + 4)^ 2 + ( x + 1) \cdot ( x + 2) = 9 $

b) Oldja meg az alábbi egyenletrendszert a valós számpárok halmazán!

$ \begin{cases} 2x + y = 7 \\ 3x - 7 y = 36  \end{cases} $

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Az $ ABCD $ derékszögű trapéz $ 6 $ cm-es $ BC $ szára $ 110^ \circ $-os szöget zár be a $ 12 $ cm-es $ CD $ alappal.

a) Számítsa ki a trapéz másik két oldalának a hosszát!
b) Számítsa ki a $ BCD $ háromszög $ BD $ oldalának hosszát és ismeretlen szögeinek nagyságát!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Amerikai kutatók 104 labrador genetikai elemzése alapján felállítottak egy egyenletet, amellyel (a kutya 3 hónapos korától) megmondható, milyen korú az adott kutya emberévekben. A kutya valódi életkorát években mérve jelölje $ K $, ekkor az emberévekben kifejezett életkort ($ E $) az alábbi képlettel kapjuk: $ E = 37 \cdot  \lg K + 31 $ (ahol $ K > 0,25 $).
a) Egy kutya emberévekbe átszámított életkora $ E = 70 $ év. Hány év, hány hónap ennek a kutyának a valódi életkora? Válaszát egész hónapra kerekítve adja meg!
Egy másik átszámítás szerint – a kutya 3 éves korától kezdve – az emberévekben kifejezett életkor az $ e = 5,5 \cdot K + 12 $  képlettel kapható meg (ahol $ K > 3 $).
b) Számítsa ki egy $ K = 8 $ éves labrador esetén az emberévekben kifejezett életkort mindkét képlettel! Az amerikai kutatók képletéből kiszámított érték hány százalékkal nagyobb, mint a másik képletből kiszámított érték?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Egy nyolccsapatos jégkorongbajnokságban minden csapat minden másikkal egyszer mérkőzik meg. Az ábrán látható gráf az eddig lejátszott mérkőzéseket szemlélteti. A pontok a csapatokat jelképezik, és két pont között pontosan akkor van él, ha a két csapat már játszott egymással.
A bajnokságból 5 fordulót már megrendeztek, ám néhány mérkőzés elmaradt. (Egy fordulóban – ha nincs elmaradó mérkőzés – mindegyik csapat egy mérkőzést játszik.)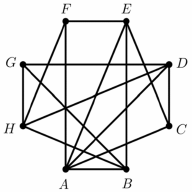

a) Adja meg három olyan csapat betűjelét, melyek közül bármely kettő már lejátszotta az egymás közötti mérkőzését!
b) Hány mérkőzés maradt el az első 5 fordulóban?
Az egyik játékos 0,3 valószínűséggel szerez gólt egy büntetőlövésből.
c) Mekkora a valószínűsége, hogy 10 büntetőlövésből pontosan 4 gólt szerez?
A szabványos jégkorong egy olyan vulkanizált gumihenger, amelynek magassága 2,54 cm (1 inch), alapkörének átmérője 7,62 cm (3 inch). Az egyik csapat a pálya bejáratához egy olyan nagyméretű korongot terveztet, amely (matematikai értelemben) hasonló a szabványos jégkoronghoz. A tervben szereplő nagyméretű korong térfogata 1 m 3.

d) Számítsa ki a nagyméretű korong magasságának és alapköre átmérőjének a hosszát!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

a) Az $ x \rightarrow mx + b $ lineáris függvény $ 1 $-hez $ 200 $-at, $ 21 $-hez pedig $ 5200 $-at rendel. Adja meg $ m $ és $ b $ értékét!
Anna szeretne részt venni a Balaton-átúszáson, amelyhez két különböző 21 napos edzéstervet készít. Azt már elhatározta, hogy az első napon 200 métert, az utolsó, 21. naponpedig az átúszás teljes távját, 5200 métert úszik. Az egyik edzéstervben a napi úszásmennyiségek egy számtani sorozat egymást követő tagjai, a másik változatban pedig (jó közelítéssel) egy mértani sorozaté.
b) A teljes felkészülés alatt összesen hány métert úszna Anna az egyik, illetve a másik változatban?
A 2020-as Balaton-átúszáson az indulók $ 36\% $-a volt nő, átlagéletkoruk 35 év. Az indulók $ 64\% $-a volt férfi, átlagéletkoruk 38 év.
c) Mennyi volt ebben az évben az összes induló átlagéletkora?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Az ábrán szereplő $ A, B, C, D $ és $ E $ pontok egy olyan egyenesre illeszkednek, amely párhuzamos az $ F $ és $ G $ pontokra illeszkedő egyenessel.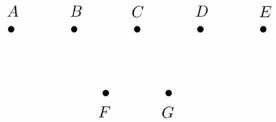

a) Hány olyan különböző egyenes létezik, amely az ábrán lévő pontok közül legalább kettőre illeszkedik?
b) Hány olyan háromszög van, amelynek a csúcsait az ábrán szereplő 7 pont közül választjuk ki? (Két háromszöget különbözőnek tekintünk, ha legalább az egyik csúcsukban eltérnek egymástól.)
Egy háromszög csúcsai: $ K(– 1; 5) $, $ L(1; 1) $, $ M(5; 3) $.
c) Igazolja, hogy a háromszög L-nél lévő szöge derékszög!
d) Írja fel a háromszög körülírt körének az egyenletét!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba