(Feladat azonosítója: mmk_202105_2r16f )
Témakör: *Algebra
Egy nyolccsapatos jégkorongbajnokságban minden csapat minden másikkal egyszer mérkőzik meg. Az ábrán látható gráf az eddig lejátszott mérkőzéseket szemlélteti. A pontok a csapatokat jelképezik, és két pont között pontosan akkor van él, ha a két csapat már játszott egymással.
A bajnokságból 5 fordulót már megrendeztek, ám néhány mérkőzés elmaradt. (Egy fordulóban – ha nincs elmaradó mérkőzés – mindegyik csapat egy mérkőzést játszik.)
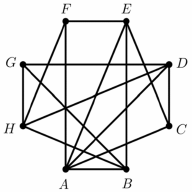 a) Adja meg három olyan csapat betűjelét, melyek közül bármely kettő már lejátszotta az egymás közötti mérkőzését!
a) Adja meg három olyan csapat betűjelét, melyek közül bármely kettő már lejátszotta az egymás közötti mérkőzését!
b) Hány mérkőzés maradt el az első 5 fordulóban?
Az egyik játékos 0,3 valószínűséggel szerez gólt egy büntetőlövésből.
c) Mekkora a valószínűsége, hogy 10 büntetőlövésből pontosan 4 gólt szerez?
A szabványos jégkorong egy olyan vulkanizált gumihenger, amelynek magassága 2,54 cm (1 inch), alapkörének átmérője 7,62 cm (3 inch). Az egyik csapat a pálya bejáratához egy olyan nagyméretű korongot terveztet, amely (matematikai értelemben) hasonló a szabványos jégkoronghoz. A tervben szereplő nagyméretű korong térfogata 1 m 3.

d) Számítsa ki a nagyméretű korong magasságának és alapköre átmérőjének a hosszát!
Megoldás:
a) Egy betűhármas megadása az $ \left\{ABE, ACD, ACE, AEF, BGH, DGH \right\} $ halmazból.
b) 5 mérkőzés
c) $ \approx 0,2 $
d) Magassága: $ \approx 52 $ cm,
alapkörének átmérője: $ \approx 156 $ cm.