1. találat: Matematika középszintű érettségi, 2017. május, II. rész, 13. feladat
Témakör: *Függvények (másodfokú, algebra, egyenlet) (Azonosító: mmk_201705_2r13f )
Adott a valós számok halmazán értelmezett $ f $ függvény:$ x \mapsto (x-1)^2-4 $.
a) Számítsa ki az $ f $ függvény $ x=-5 $ helyen felvett helyettesítési értékét!
b) Ábrázolja az $ f $ függvényt, és adja meg szélsőértékének helyét és értékét!
c) Oldja meg a következő egyenletet a valós számok halmazán: $ (x-1)^2-4=-x-1 $
*Geometria (Thalesz-tétel, terület, hasonlóság, arány, Pitagorasz-tétel, befogótétel) (Azonosító: mmk_201705_2r14f )
Az ABC derékszögű háromszög egyik befogója 8 cm, átfogója 17 cm hosszú.
a) Számítsa ki a háromszög 17 cm-es oldalához tartozó magasságának hosszát!
b) Hány $ cm^2 $ a háromszög körülírt körének területe?
A DEF háromszög hasonló az ABC háromszöghöz, és az átfogója 13,6 cm hosszú.
c) Hány százaléka a DEF háromszög területe az ABC háromszög területének?
*Sorozatok (statisztika, számtani sorozat, kördiagram) (Azonosító: mmk_201705_2r15f )
Az alábbi kördiagram egy balatoni strandon a júliusban megvásárolt belépőjegyek típusának eloszlását mutatja. Júliusban összesen 16 416 fő vásárolt belépőjegyet. A belépőjegyek árát az alábbi táblázat tartalmazza.
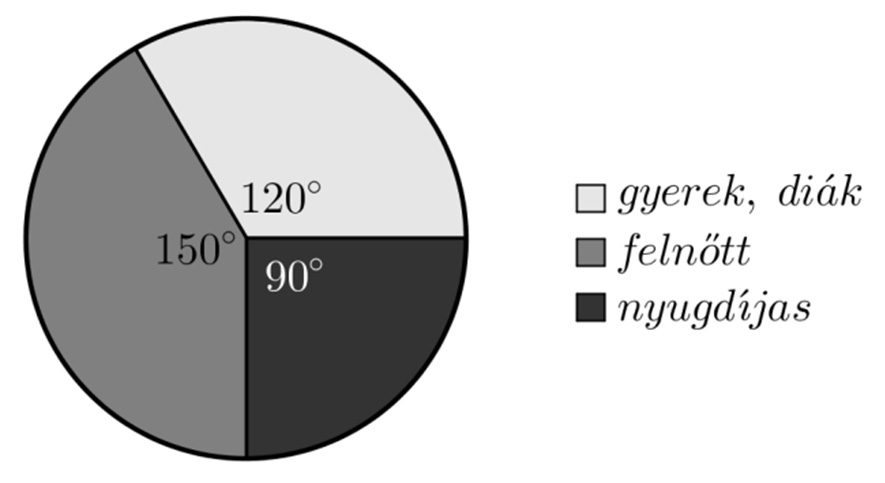
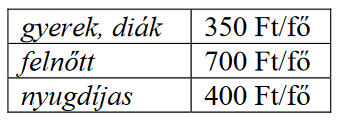
a) Mennyi volt a strand bevétele a júliusban eladott belépőkből?
A tapasztalatok szerint júliusban folyamatosan nő a strandolók száma. Ezért a strandbüfében bevált rendszer, hogy a július 1-jei megrendelést követően július 2-től kezdve július 31-ig minden nap ugyanannyi literrel növelik a nagykereskedésből megrendelt üdítő mennyiségét.
A könyvelésből kiderült, hogy július 1-jén, 2-án és 3-án összesen 165 litert, július 15-én pedig 198 litert rendeltek.
b) Hány liter üdítőt rendeltek júliusban összesen?
*Koordináta-geometria (metszéspont, egyenes, kör) (Azonosító: mmk_201705_2r16f )
Adott két pont a koordinátasíkon: A(2; 6) és B(4; -2).
a) Írja fel az AB szakasz felezőmerőlegesének egyenletét!
b) Írja fel az A ponton átmenő, B középpontú kör egyenletét!
Adott az $ y = 3x $ egyenletű egyenes és az $ x^2+8x+y^2-4y=48 $ egyenletű kör.
c) Adja meg koordinátáikkal az egyenes és a kör közös pontjait!
*Térgeometria (térfogat, négyzetes hasáb, százalék, kombinatorika, valószínűség) (Azonosító: mmk_201705_2r17f )
A Hód Kft. faárutelephelyén rönkfából (henger alakú fatörzsekből) a következő módon készítenek gerendát. A keretfűrészgép először két oldalt levág egy-egy – az ábrán sötéttel jelölt – részt, majd a fa 90°-kal történő elfordítása után egy hasonló vágással végül egy négyzetes hasáb alakú gerendát készít.
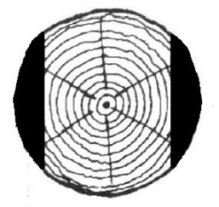
A gépet úgy állítják be, hogy a kapott hasáb alaplapja a lehető legnagyobb legyen. Most egy forgáshenger alakú, 60 cm átmérőjű, 5 méter hosszú rönkfát fűrészel így a gép.
a) Igaz-e, hogy a kapott négyzetes hasáb alakú fagerenda térfogata kisebb 1 köbméternél?
A Hód Kft. deszkaárut is gyárt, ehhez a faanyagot $ 30 000 Ft/m^3 $-es beszerzési áron vásárolja meg a termelőtől. A gyártás közben a megvásárolt fa kb. 40%-ából hulladékfa lesz. A késztermék 1 köbméterét 90 000 forintért adja el a cég, de az eladási ár 35%-át a költségekre kell fordítania (feldolgozás, telephely fenntartása stb.).
b) Mennyi haszna keletkezik a Hód Kft.-nek 1 köbméter deszkaáru eladásakor?
A fakitermelő cég telephelyéről hat teherautó indul el egymás után. Négy teherautó fenyőfát, kettő pedig tölgyfát szállít.
c) Számítsa ki annak a valószínűségét, hogy a két, tölgyfát szállító teherautó közvetlenül egymás után gördül ki a telephelyről, ha az autók indulási sorrendje véletlenszerű!
*Logika (halmazok, szita formula, kombinatorika, valószínűség, statisztika) (Azonosító: mmk_201705_2r18f )
Egy 20 fős társaság tagjait az április havi szabadidős tevékenységeikről kérdezték. Mindenki három eldöntendő kérdésre válaszolt (igennel vagy nemmel).
I. Volt-e moziban?
II. Olvasott-e szépirodalmi könyvet?
III. Volt-e koncerten?
A válaszokból kiderült, hogy tizenketten voltak moziban, kilencen olvastak szépirodalmi könyvet, és négy fő járt koncerten. Öten voltak, akik moziban jártak és szépirodalmi könyvet is olvastak, négyen pedig moziban és koncerten is jártak. Hárman mindhárom kérdésre igennel válaszoltak.
a) Hány olyan tagja van a társaságnak, aki mindhárom kérdésre nemmel válaszolt?
A társaság 20 tagja közül véletlenszerűen kiválasztunk kettőt.
b) Számítsa ki annak a valószínűségét, hogy legalább az egyikük volt moziban április folyamán! Attól a kilenc személytől, akik olvastak áprilisban szépirodalmi könyvet, azt is megkérdezték, hogy hány könyvet olvastak el a hónapban. A válaszok (pozitív egész számok) elemzése után kiderült, hogy a kilenc szám (egyetlen) módusza 1, mediánja 2, átlaga $ \dfrac{16}{9} $ terjedelme pedig 2.
c) Adja meg ezt a kilenc számot!


