1. találat: Matematika középszintű érettségi, 2010. május, II. rész, 13. feladat
Témakör: *Algebra (Azonosító: mmk_201005_2r13f )
Számítsa ki azt a két pozitív számot, amelyek számtani (aritmetikai) közepe 8, mértani (geometriai) közepe pedig 4,8.
*Geometria (Azonosító: mmk_201005_2r14f )
Az $ ABC $ háromszög csúcspontjainak koordinátái: $ A(0; 0), B(–2; 4), C(4; 5) $.
a) Írja fel az $ A $B oldal egyenesének egyenletét!
b) Számítsa ki az $ ABC$ háromszög legnagyobb szögét! A választ tized fokra kerekítve adja meg!
c) Számítsa ki az $ ABC $ háromszög területét!
*Geometria (Azonosító: mmk_201005_2r15f )
a) Rajzolja meg derékszögű koordinátarendszerben a $ ]-1;6 ] $ intervallumon értelmezett, $ -\left|x-2 \right|+3 $ hozzárendelésű függvény grafikonját!
b) Állapítsa meg a függvény értékkészletét, és adja meg az összes zérushelyét!
c) Döntse el, hogy a $ P(3,2 ; 1,85) $ pont rajta van-e a függvény grafikonján! Válaszát számítással indokolja!
d) Töltse ki az alábbi táblázatot, és adja meg a függvényértékek (a hét szám) mediánját!

*Kombinatorika (Azonosító: mmk_201005_2r16f )
Egy középiskolába 620 tanuló jár. Az iskola diákbizottsága az iskolanapra három kiadványt jelentetett meg:
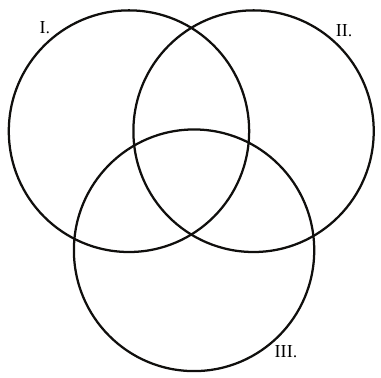
I. Diákok Hangja
II. Iskolaélet
III. Miénk a suli!
Később felmérték, hogy ezeknek a kiadványoknak milyen volt az olvasottsága az iskola tanulóinak körében. A Diákok Hangját a tanulók $ 25\% $-a, az Iskolaéletet $ 40\% $-a, a Miénk a suli! c. kiadványt pedig $ 45\% $-a olvasta. Az első két kiadványt a tanulók $ 10\% $-a, az első és harmadik kiadványt $ 20\% $-a, a másodikat és harmadikat $ 25\% $-a, mindhármat pedig $ 5\% $-a olvasta.
a) Hányan olvasták mindhárom kiadványt?
b) A halmazábra az egyes kiadványokat elolvasott tanulók létszámát szemlélteti. Írja be a halmazábra mindegyik tartományába az oda tartozó tanulók számát!
c) Az iskola tanulóinak hány százaléka olvasta legalább az egyik kiadványt?
Az iskola 12. évfolyamára 126 tanuló jár, közöttük kétszer annyi látogatta az iskolanap rendezvényeit, mint aki nem látogatta. Az Iskolaélet című kiadványt a rendezvényeket látogatók harmada, a nem látogatóknak pedig a fele olvasta. Egy újságíró megkérdez két, találomra kiválasztott diákot az évfolyamról, hogy olvasták-e az Iskolaéletet.
d) Mekkora annak a valószínűsége, hogy a két megkérdezett diák közül az egyik látogatta az iskolanap rendezvényeit, a másik nem, viszont mindketten olvasták az Iskolaéletet?
*Kombinatorika (Azonosító: mmk_201005_2r17f )
Statisztikai adatok szerint az 1997-es év utáni években 2003-mal bezárólag a világon évente átlagosan $ 1,1\% $-kal több autót gyártottak, mint a megelőző évben. A 2003-at követő években, egészen 2007-tel bezárólag évente átlagosan már $ 5,4\% $-kal gyártottak többet, mint a megelőző évben. 2003-ban összesen 41,9 millió autó készült.
a) Hány autót gyártottak a világon 2007-ben?
b) Hány autót gyártottak a világon 1997-ben? Válaszait százezerre kerekítve adja meg!
2008-ban az előző évhez képest csökkent a gyártott autók száma, ekkor a világon összesen 48,8 millió új autó hagyta el a gyárakat. 2008-ban előrejelzés készült a következő 5 évre vonatkozóan. Eszerint 2013-ban 38 millió autót fognak gyártani. Az előrejelzés úgy számolt, hogy minden évben az előző évinek ugyanakkora százalékával csökken a termelés.
c) Hány százalékkal csökken az előrejelzés szerint az évenkénti termelés a 2008-at követő 5 év során? Az eredményt egy tizedes jegyre kerekítve adja meg!
d) Elfogadjuk az előrejelzés adatát, majd azt feltételezzük, hogy 2013 után évente $ 3\% $-kal csökken a gyártott autók száma. Melyik évben lesz így az abban az évben gyártott autók száma a 2013-ban gyártottaknak a $ 76\% $-a?
*Geometria (Azonosító: mmk_201005_2r18f )
Az egyik csokoládégyárban egy újfajta, kúp alakú desszertet gyártanak. A desszert csokoládéból készült váza olyan, mint egy tölcsér. (Lásd ábra.) A külső és belső kúp hasonló, a hasonlóság aránya $ \dfrac{6}{ 5} $ . A kisebb kúp adatai: alapkörének sugara 1 cm, magassága 2,5 cm hosszú.
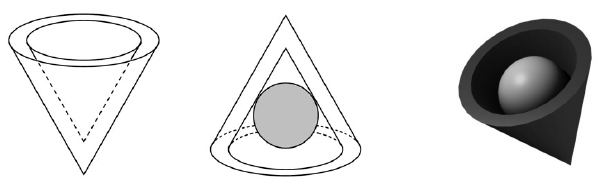
a) Hány cm3 csokoládét tartalmaz egy ilyen csokoládéváz? A választ tizedre kerekítve adja meg!
Az elkészült csokoládéváz üreges belsejébe marcipángömböt helyeznek, ezután egy csokoládéból készült vékony körlemezzel lezárják a kúpot.
b) Hány cm a sugara a lehető legnagyobb méretű ilyen marcipángömbnek? A választ tizedre kerekítve adja meg!
A marcipángömböket gyártó gép működése nem volt hibátlan. A mintavétellel végzett minőség-ellenőrzés kiderítette, hogy a legyártott gömbök $ 10\% $-ában a marcipángömb mérete nem felel meg az előírtnak.
c) A már legyártott nagy mennyiségű gömb közül 10-et kiválasztva, mekkora annak a valószínűsége, hogy a kiválasztottak között pontosan 4-nek a mérete nem felel meg az előírásnak? (A kérdezett valószínűség kiszámításához használhatja a binomiális eloszlás képletét.)


