Az egyik csokoládégyárban egy újfajta, kúp alakú desszertet gyártanak. A desszert csokoládéból készült váza olyan, mint egy tölcsér. (Lásd ábra.) A külső és belső kúp hasonló, a hasonlóság aránya $ \frac{6}{ 5} $ . A kisebb kúp adatai: alapkörének sugara 1 cm, magassága 2,5 cm hosszú.

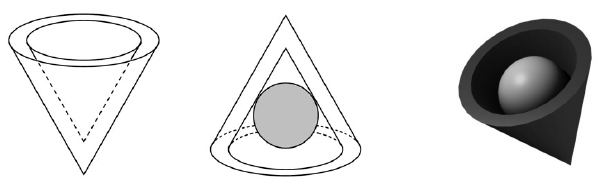
a) Hány cm3 csokoládét tartalmaz egy ilyen csokoládéváz? A választ tizedre kerekítve adja meg!

Az elkészült csokoládéváz üreges belsejébe marcipángömböt helyeznek, ezután egy csokoládéból készült vékony körlemezzel lezárják a kúpot.

b) Hány cm a sugara a lehető legnagyobb méretű ilyen marcipángömbnek? A választ tizedre kerekítve adja meg!

A marcipángömböket gyártó gép működése nem volt hibátlan. A mintavétellel végzett minőség-ellenőrzés kiderítette, hogy a legyártott gömbök $ 10\% $-ában a marcipángömb mérete nem felel meg az előírtnak.

c) A már legyártott nagy mennyiségű gömb közül 10-et kiválasztva, mekkora annak a valószínűsége, hogy a kiválasztottak között pontosan 4-nek a mérete nem felel meg az előírásnak? (A kérdezett valószínűség kiszámításához használhatja a binomiális eloszlás képletét.)

Megoldás:

a) Egy csokoládéváz kb. $ 1,9\ cm^3 $ csokoládét tartalmaz.

b) Tehát a lehető legnagyobb marcipángömb sugara kb. 0,7 cm.

c) $P\approx 0,011 $