Adott a $ C(-6; -2)  $ és a $ P(-3; 2)  é pont.

a) Írja fel a  $ C $ középpontú, $ P $ ponton átmenő k kör egyenletét!

b) Írja fel a $ k $ kör $ P $ pontra illeszkedő érintőegyenesének egyenletét!

A $ C $ és $ P $ pontokon áthaladó egyenes és a két koordinátatengely egy derékszögű háromszöget határoz meg.

c) Határozza meg a háromszög köré írható kör sugarának hosszát!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Oldja meg az alábbi egyenleteket a valós számok halmazán!

a) $ \sin^2 x = 3\cos^2 x $

b) $ \log_3 ( x + 8) + \log_3 ( x − 2) − \log_3 ( x + 4) = 1 $

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Egy napelemes akkumulátortöltőket gyártó cég termékei közül 24 darabnak az élettartamát vizsgálták. A vizsgálat végeredményét (a 24 darabra vonatkozóan) az alábbi kördiagram szemlélteti.

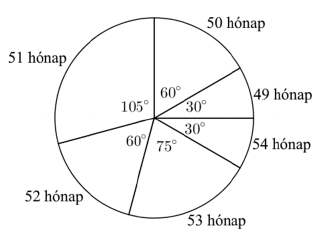
a)Töltse ki az alábbi táblázatot, és határozza meg a 24 darab töltő élettartamának átlagát és szórását!

A részletesebb vizsgálatok szerint a cég által gyártott töltők 90 százaléka legalább 50 hónap élettartamú (ezt tekinthetjük úgy, hogy egy véletlenszerűen kiválasztott töltő 0,9 valószínűséggel legalább 50 hónap élettartamú).
b) Mekkora a valószínűsége annak, hogy egy szakboltba kiszállított 20 darab töltő között legfeljebb kettő olyan található, amelynek az élettartama 50 hónapnál kevesebb?
Ismert az is, hogy 0,75 annak a valószínűsége, hogy öt darab véletlenszerűen kiválasztott töltő mindegyikének élettartama 55 hónapnál kevesebb.
c)Mekkora a valószínűsége annak, hogy egy darab véletlenszerűen kiválasztott töltő élettartama legalább 55 hónap?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Adott az $ f(x) = \sin x $ és a $ g(x) = \left(\dfrac{2x}{\pi}\right)^2 $ függvény ($ x \in \mathbb{R} $).

a) Igazolja, hogy mindkét függvény grafikonja áthalad az origón és a $ \left(\dfrac{\pi}{2};1\right) $

b) Határozza meg a két függvény grafikonja által közbezárt síkidom területét, ha $ x \in \left[0;\dfrac{\pi}{2}\right] $

Adott az $ a_n = \dfrac{2+2\pi n}{n} $ ($ n \in \mathbb{N}^+ $ ).

c) Igazolja, hogy ez a sorozat szigorúan monoton csökkenő és korlátos, és adja meg a sorozat határértékét!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba