a) Oldja meg az alábbi egyenletrendszert, ahol x és y pozitív valós számok!

$\begin{cases}x+y=0,2\\ \dfrac{\lg x+\lg y}{2}=\lg\dfrac{x+y}{2} \end{cases}$

b) Oldja meg a $ [-\pi;\pi] $ halmazon a $ 2\sin^2x-\cos x=2 $ egyenletet!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Két várost egy 195 km hosszú vasútvonal köt össze. Ezen a vonalon személyvonattal is és gyorsvonattal is el lehet jutni egyik városból a másikba. A személyvonat átlagsebessége 18 km/h-val kisebb a gyorsvonaténál, menetideje így 45 perccel több.

a) Határozza meg a vonatok átlagsebességét!

Az egyik hét munkanapjain utasszámlálást végeztek a személyvonaton. Hétfőn 200, kedden 160, szerdán 90, csütörtökön 150 utast jegyeztek fel.

b) Hány utas volt pénteken, ha tudjuk, hogy az öt adat átlaga is szerepel az adatok között, továbbá az adatok (egyetlen) módusza nem egyenlő a mediánjukkal?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

a) Az ABCD négyzet körülírt körén felvettünk egy olyan P pontot, amelyik nem csúcsa a négyzetnek. Bizonyítsa be, hogy $ AP^2+CP^2=BP^2+DP^2 $.

Egy cég az általa forgalmazott poharakat négyesével csomagolja úgy, hogy a poharakhoz még egy tálcát is ad ajándékba. A 20 cm (belső) átmérőjű, felül nyitott forgáshenger alakú tálcára négy egyforma (szintén forgáshenger alakú) poharat tesznek úgy, hogy azok szorosan illeszkednek egymáshoz és a tálca oldalfalához is.

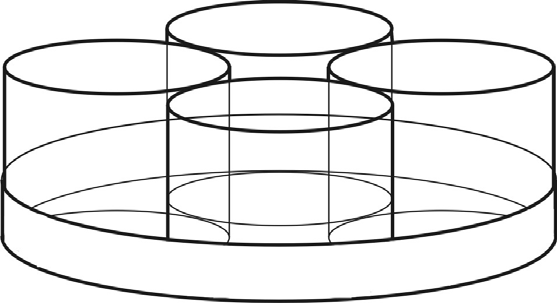
b) Igazolja, hogy a poharak alapkörének sugara nagyobb 4,1 cm-nél!

A pohár fala 2,5 mm vastag, belső magassága 11 cm.

c) Igaz-e, hogy a pohárba belefér 5 dl üdítő?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Az $ f:\mathbb{R}\rightarrow \mathbb{R}, f(x)=x^2-12x+27 $ függvény grafikonja a derékszögű koordináta-rendszerben parabola.

a) Számítsa ki a parabola és az x tengely által bezárt (korlátos) síkidom területét!

b) Írja fel a parabolához az E(5;-8) pontjában húzott érintő egyenletét!

c) Számítsa ki a parabola fókuszpontjának koordinátáit!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba