a) Az ABCD négyzet körülírt körén felvettünk egy olyan P pontot, amelyik nem csúcsa a négyzetnek. Bizonyítsa be, hogy $ AP^2+CP^2=BP^2+DP^2 $.

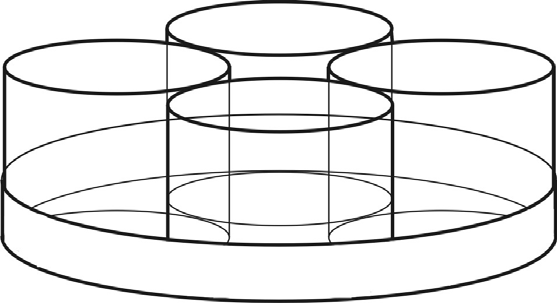
Egy cég az általa forgalmazott poharakat négyesével csomagolja úgy, hogy a poharakhoz még egy tálcát is ad ajándékba. A 20 cm (belső) átmérőjű, felül nyitott forgáshenger alakú tálcára négy egyforma (szintén forgáshenger alakú) poharat tesznek úgy, hogy azok szorosan illeszkednek egymáshoz és a tálca oldalfalához is.

b) Igazolja, hogy a poharak alapkörének sugara nagyobb 4,1 cm-nél!

A pohár fala 2,5 mm vastag, belső magassága 11 cm.

c) Igaz-e, hogy a pohárba belefér 5 dl üdítő?

Megoldás:

b) $ r=\dfrac{10}{1+\sqrt{2}} $

c) $ V=523cm^3 $, tehát igaz.