a) Adja meg az $ 5x^2+5y^2-14x+22y-11=0 $ egyenletű kör középpontját és sugarát!

Adott a k kör, amelynek középpontja a K(–5; 7) pont, és a sugara 10 egység. Ezen a körön belül adott az A(−4; 14) pont.

b) Írja fel annak az A ponton áthaladó e egyenesnek az egyenletét, amely merőleges a KA szakaszra!

c) Határozza meg a k kör e egyenesre illeszkedő húrjának hosszát!

A koordináta-rendszer P(x; y) pontját rácspontnak nevezzük, ha x és y egész számok.

d) Hány rácsponton megy át a k körvonal?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

A 11. b osztály a következő tanévre nyolc kötelező olvasmányt kapott. Ezek közül kettő ugyanannak a szerzőnek a munkája, a többi szerzőnek csak egy-egy könyve van az olvasmányok között. Andi még nyáron szeretne elolvasni a nyolc könyv közül hármat. A nyarat a nagyszüleinél tölti, ezért a kiválasztott három könyvet magával viszi.

a) Hányféleképpen választhatja ki Andi, hogy melyik három könyvet vigye magával, ha azt szeretné, hogy a három könyv három különböző szerző műve legyen?

Az osztály tanulói közül hatan: Andi, Barbara, Csilla, Dani, Elek és Feri moziba mennek.

b) Hányféleképpen ülhetnek le hat egymás melletti székre úgy, hogy semelyik két lány ne üljön egymás mellett?

Három lány és n fiú véletlenszerű elrendezésben leül egy sorba.

c) Határozza meg n értékét, ha $ \dfrac{1}{26} $ annak a valószínűsége, hogy a három lány egymás mellett ül!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Adott a valós számok halmazán értelmezett f és g függvény:

$ f(x)=x^2-2 $ és $ g(x)=10+10x-x^2 $

a) Oldja meg a valós számok halmazán az $ \left| f(x) + g(x)\right| \geq 8 $ egyenlőtlenséget!

b) Igazolja, hogy a [2; 8] intervallumon az f és a g függvény is csak pozitív értékeket vesz fel!

c) Határozza meg azt a t valós számot a [2; 8] intervallumban, amelyre teljesül, hogy az f függvény görbéje alatti terület a [2; t] intervallumon megegyezik a g függvény görbéje alatti területtel a [t; 8] intervallumon.

(Egy [a; b] intervallumon folytonos függvény görbéje alatti terület ezen az intervallumon megegyezik az x tengely, az x = a, az x = b egyenletű egyenesek és a függvény grafikonja által meghatározott síkidom területével.)

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Egy színházban a jegyek az I., a II. vagy a III. árkategóriába tartoznak. Az egyik esti előadásra összesen 200 jegyet adtak el. Az eladott jegyek között a III. árkategóriájúak száma a másik két árkategóriába tartozó jegyek együttes számának kétharmada, az I., illetve II. árkategóriájú jegyek számának aránya pedig 9:11 volt.

a) Hány jegyet adtak el az egyes árkategóriákban?

Egy várrom területén szabadtéri színházat alakítanak ki. A tervrajz szerint a téglalap alakú színpadot az egyik bástya félkör alakban elhelyezkedő falmaradványai közé helyeznék el. A bástya belső átmérője 12 méter. (Az ábrán a tervrajz egy részlete látható: O a félkör középpontja, a téglalap csúcsába vezető sugár és az átmérő közötti szög pedig $ \alpha $; $ 0<\alpha<2\pi $.)

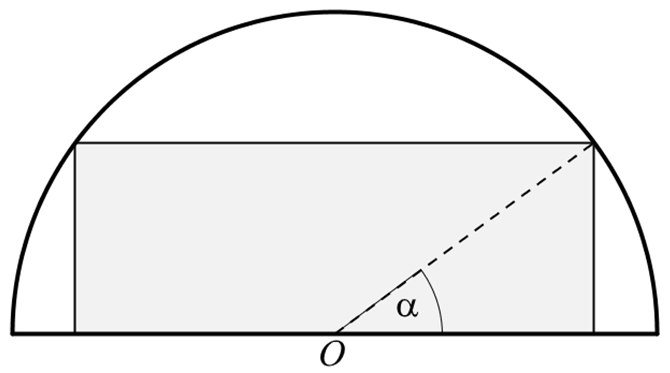
b) Hogyan kell megválasztani az $ \alpha $ szöget, hogy a színpad területe a lehető legnagyobb legyen? Mekkora ez a legnagyobb terület?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

a) Egy számtani sorozat első tagja 4, differenciája 5. Egy mértani sorozat első tagja 3, hányadosa 2. Az 1000-nél kisebb pozitív egészek közül egyet véletlenszerűen kiválasztunk.

Mekkora a valószínűsége, hogy olyan számot választottunk, amely tagja valamelyik sorozatnak?

Válaszát $ \dfrac{p}{q} $ alakban adja meg úgy, hogy p és q pozitív egészek és relatív prímek legyenek!

b) Három teljes gráf pontjainak száma egy növekvő számtani sorozat három egymást követő tagja. Igazolja, hogy a három gráf éleinek száma ekkor nem lehet egy számtani sorozat három egymást követő tagja! (Teljes gráf: olyan egyszerű gráf, melynek bármely két pontja között van él.)

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba