Egy színházban a jegyek az I., a II. vagy a III. árkategóriába tartoznak. Az egyik esti előadásra összesen 200 jegyet adtak el. Az eladott jegyek között a III. árkategóriájúak száma a másik két árkategóriába tartozó jegyek együttes számának kétharmada, az I., illetve II. árkategóriájú jegyek számának aránya pedig 9:11 volt.

a) Hány jegyet adtak el az egyes árkategóriákban?

Egy várrom területén szabadtéri színházat alakítanak ki. A tervrajz szerint a téglalap alakú színpadot az egyik bástya félkör alakban elhelyezkedő falmaradványai közé helyeznék el. A bástya belső átmérője 12 méter. (Az ábrán a tervrajz egy részlete látható: O a félkör középpontja, a téglalap csúcsába vezető sugár és az átmérő közötti szög pedig $ \alpha $; $ 0<\alpha<2\pi $.)

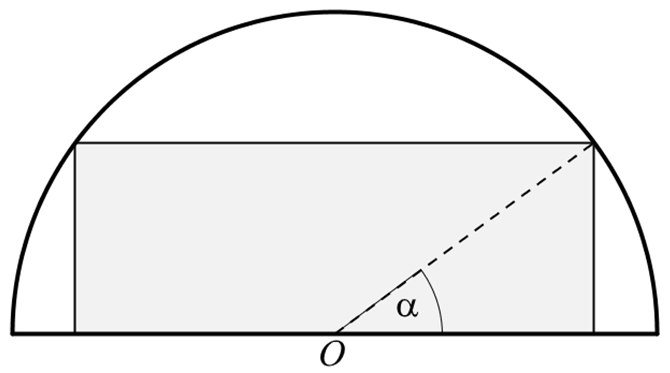
b) Hogyan kell megválasztani az $ \alpha $ szöget, hogy a színpad területe a lehető legnagyobb legyen? Mekkora ez a legnagyobb terület?

Megoldás:

a)  I. kategóriás jegyből 54-et, II. kategóriásból 66-ot, III. kategóriásból pedig 80-at adtak el.

b)  $ \dfrac{\pi}{4}; 36. $