A $ x^2 = 2 y $ egyenletű parabola az $ x^2 + y^2\le 8 $egyenletű körlapot két részre vágja. Mekkora a konvex rész területe? Számolása során ne használja a $ \pi $ közelítő értékét!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Megrajzoltuk az ABCDE szabályos ötszöget, és berajzoltuk minden átlóját. Az átlók metszéspontjait az ábra szerint betűztük meg: P, Q, R, S, T.

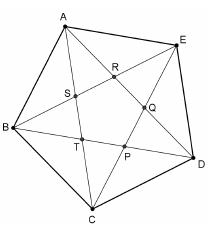
a) Hány olyan háromszög látható az ábrán, amelynek mindhárom csúcsa a megjelölt 10 pont közül való, és mindhárom oldalegyenese az ABCDE ötszög oldalegyenesei és átlóegyenesei közül kerül ki? Hány lényegesen különböző háromszög van ezek között, ha az egymáshoz hasonló háromszögeket nem tekintjük lényegesen különbözőknek?

b) Tudjuk, hogy az ABCQ négyszög területe 120 cm2 . Mekkora az ABCDE ötszög területe? Válaszát egész értékre kerekítve adja meg!

c) Tekintsük azt a tíz csúcsú gráfot, amelyet a megadott ábra szemléltet. Erről a gráfról fogalmaztunk meg két állítást. Állapítsa meg mindkét állításról, hogy igaz vagy hamis! Adjon rövid magyarázatot válaszára!

1. állítás: Ennek a gráfnak 20 éle van.

2. állítás: Ebben a gráfban van olyan részgráf, amely nyolc élű kör.

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Egy kozmetikumokat gyártó vállalkozás nagy tételben gyárt egyfajta krémet. A termelés teljes havi mennyisége (x kilogramm) 100 és 700 kg közé esik, amelyet egy megállapodás alapján a gyártás hónapjában el is adnak egy nagykereskedőnek. A megállapodás azt is tartalmazza, hogy egy kilogramm krém eladási ára: $ (36-0,03x) $ euró. A krémgyártással összefüggő havi kiadás (költség) is függ a havonta eladott mennyiségtől. A krémgyártással összefüggő összes havi kiadást (költséget) a $ 0 , 0001 x ^{3} - 30 , 12 x + 13 000 $ összefüggés adja meg, szintén euróban.

a) Számítsa ki, hogy hány kilogramm krém eladása esetén lesz az eladásból származó havi bevétel a legnagyobb! Mekkora a legnagyobb havi bevétel?

b) Adja meg a krémgyártással elérhető legnagyobb havi nyereséget! Hány kilogramm krém értékesítése esetén valósul ez meg? (nyereség=bevétel–kiadás)

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

a) Két gyerek mindegyike 240 forintért vett kaparós sorsjegyet. Fémpénzzel fizettek (5; 10, 20, 50, 100 és 200 forintos érmékkel), és pontoson kiszámolták a fizetendő összeget. Hányféleképpen fizethetett Miki, ha ő 4 darab érmével fizetett, és hányféleképpen fizethet Karcsi, ha ő 5 darab érmével fizetett? (A pénzérmék átadási sorrendjét nem vesszük figyelembe.) A "bergengóc" lottóban kétszer húznak egy játéknapon. Bandi egy szelvénnyel játszik, tehát az adott játéknapon mindkét húzásnál nyerhet ugyanazzal a szelvénnyel.

b) Mekkora annak a valószínűsége, hogy egy adott játéknapon Bandinak legalább egy telitalálata lesz, ha $ p $ annak a valószínűsége $ ( 0 < p < 1 ) $, hogy egy szelvényen, egy húzás esetén telitalálata lesz? Megváltoztatták a játékszabályokat: minden játéknapon csak egyszer húznak (más játékszabály nem változott). Bandi most két (nem feltétlenül különbözően kitöltött) szelvénnyel játszik.

c) Mekkora annak a valószínűsége, hogy egy adott játéknapon Bandinak telitalálata legyen valamelyik szelvényén?

d) A telitalálat szempontjából a b) vagy a c)-ben leírt játék kedvezőbb Bandi számára?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Egy egyetem 10 580 hallgatójának tanulmányi lapjáról összesítették az angol és német nyelvvizsgák számát. Kiderült, hogy a német nyelvvizsgával nem rendelkezők $ 70\% $-ának, a német nyelvvizsgával rendelkezők $ 30\% $-ának nincs angol nyelvvizsgája. Az angol nyelvvizsgával nem rendelkezők $ 60\% $-ának német nyelvvizsgája sincs.

a) Ezek közül a hallgatók közül hányan rendelkeztek angol és hányan német nyelvvizsgával?

b) A hallgatók hány százaléka rendelkezett az angol és német nyelvvizsgák mindegyikével?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba