Megrajzoltuk az ABCDE szabályos ötszöget, és berajzoltuk minden átlóját. Az átlók metszéspontjait az ábra szerint betűztük meg: P, Q, R, S, T.

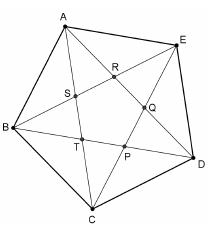
a) Hány olyan háromszög látható az ábrán, amelynek mindhárom csúcsa a megjelölt 10 pont közül való, és mindhárom oldalegyenese az ABCDE ötszög oldalegyenesei és átlóegyenesei közül kerül ki? Hány lényegesen különböző háromszög van ezek között, ha az egymáshoz hasonló háromszögeket nem tekintjük lényegesen különbözőknek?

b) Tudjuk, hogy az ABCQ négyszög területe 120 cm2 . Mekkora az ABCDE ötszög területe? Válaszát egész értékre kerekítve adja meg!

c) Tekintsük azt a tíz csúcsú gráfot, amelyet a megadott ábra szemléltet. Erről a gráfról fogalmaztunk meg két állítást. Állapítsa meg mindkét állításról, hogy igaz vagy hamis! Adjon rövid magyarázatot válaszára!

1. állítás: Ennek a gráfnak 20 éle van.

2. állítás: Ebben a gráfban van olyan részgráf, amely nyolc élű kör.

Megoldás:

a) 35 háromszög, amiből 2 lényegesen különböző

b) $ 217\ cm^2 $

c) 1. állítás: igaz, 2. állítás: igaz.