Határozzuk meg, hogy pontosan mely értékeket veheti fel az alábbi kifejezés?

$ [2a + 3b] - [a] - [b] - [a + 2b] $

Az $ a $ és $ b $ tetszőleges valós számok, $ [c] $ pedig a $ c $ egész részét jelöli.

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Határozzuk meg az összes olyan $ n $ pozitív egész számot, melyre egy $n \times n $-es táblázat mezői kitölthetők az $ 1,\ 2,\ -3 $ számokkal úgy, hogy minden sorban és minden oszlopban a számok összege $ 0 $ legyen.

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

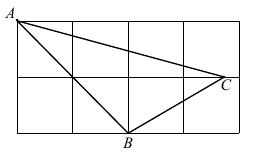
Egy $ 45^\circ $-os szöggel rendelkező $ ABC $ háromszöget az ábra szerint lerajzoltunk egy négyzethálós lapra. Határozzuk meg a háromszög másik két szögét. ($ A $ és $ B $ rácspont.)

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Nevezzük az $ n $ pozitív egész számot "prímben gazdag" számnak, ha a prímtényezős felbontásában szereplő prímek mindegyikének négyzetével is osztható. Bizonyítsuk be, hogy végtelen sok "prímben gazdag" szomszédos számpár létezik.

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Egy kör érinti az $ M $ csúcsú derékszög szárait. A szög csúcsából induló e félegyenes a kört először az $ A $, majd a $ B $ pontban metszi. A kör rövidebb $ AB $ íve a kör kerületének éppen a negyed része. Mekkora szöget zár be az e félegyenes a derékszög száraival?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba