Legyenek $ x , y $ olyan valós számok, amelyekre $ xy = 3 $ és $ x \ne y $ . Határozzuk meg azt a legnagyobb $ c $ valós számot, amelyre minden megfelelő $ x, y $ érték esetén fennáll - de nála nagyobbakra már nem -, hogy

$ \dfrac{\left[ \left( x+y\right)^2-10\right] \left[ \left( x-y\right)^2+8\right]}{\left( x-y\right)^2}\ge c $

Ezen maximális $ c $ érték mellett adjuk meg az egyenlőséget biztosító $ (x ; y ) $ számpárokat.

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

 Az $ ABCD $ konvex négyszögben $ CDA\sphericalangle = 135^\circ$,  $ BDA\sphericalangle - ABD\sphericalangle= 2\cdot D AB\sphericalangle = 4\cdot DBC \sphericalangle $ és $ BC = \sqrt{ 2 }CD$ . Igazoljuk, hogy $ AB = AD + BC $ .

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Egy $ 7 \times 7-$es tábla 4 sarokmezőjét eltávolítjuk, és a megmaradt kis négyzetek közül néhányat befestünk feketére.
a) Elérhető-e 7 mező feketére színezésével az, hogy a táblán ne maradjon teljesen fehér, kereszt alakú pentominó? (A kereszt alakú pentominó öt egybevágó kis négyzetből áll, és az alakja az ábrán látható.)

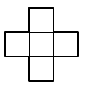
b) Biztosítható-e ugyanez, ha csak 6 mezőt festünk be feketére?
c) Igazoljuk, hogy a tábla mezőibe elhelyezhetünk egész számokat úgy, hogy bármely kereszt alakú pentominóban a számok összege negatív, míg az egész táblán szereplő számok összege pozitív.

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba