3. óra - A TENGELYES TÜKRÖZÉS TULAJDONSÁGAI
M.: Az ábrákat sokszorosítani szoktam,
szétvágom és „cetlinként” osztom az órán, mert, ha ezeket is a gyerekek
rajzolják, akkor nem fér bele egy órába.

F1.:
Tükrödet e-vel
párhuzamosan helyezd el.
-Hány szeme lehet Gerzsonnak 0,1,2,3,4,5,6
-Mitől függ, hogy páros, vagy páratlan sok szeme van? Ha a tükör rajta van egy szemen, akkor páratlan, ha nincs rajta egy szemen sem, akkor páros.
-Miért? Mert a tükör megkettőzi azokat a szemeket, melyek nincsenek a tükörvonalon, a rajta levő szemet viszont nem.
-Fogalmazd meg az észrevett tulajdonságot úgy, hogy Gerzsonról ne beszélj!
-Hány szeme lehet Gerzsonnak 0,1,2,3,4,5,6
-Mitől függ, hogy páros, vagy páratlan sok szeme van? Ha a tükör rajta van egy szemen, akkor páratlan, ha nincs rajta egy szemen sem, akkor páros.
-Miért? Mert a tükör megkettőzi azokat a szemeket, melyek nincsenek a tükörvonalon, a rajta levő szemet viszont nem.
-Fogalmazd meg az észrevett tulajdonságot úgy, hogy Gerzsonról ne beszélj!
1. A tengely minden pontjának tükörképe önmaga, a tengelyre nem illeszkedő pontokat a tükrözés megkettőzi.
Kérdés: Ismersz-e a másolópapíros eljáráson kívül más módszert, mellyel kép és tükörkép egy ábrán létrehozható?
M.: A
2. órán a másolópapíros technika bevezetése előtt is felvethetjük e
kérdést. Többnyire hoznak a gyerekek gyakorlati ötleteket már az óvodából is.
Ilyenek pl.: hajtogatott papírlapból minta kivágása (hópehely, egymás kezét
fogó kislányok sora stb.) tűvel való kiszurkálása. Szépséges terítők
készülhetnek így. Mi itt a szurkálást
szeretnénk hasznosítani, ha nem ismerik a gyerekek, mutassuk meg.
Vegyünk elő egy negyed írólapnyi „cetli”-t. (lehet
másolópapír is, vagy jegyzettömb 1-1 lapját osszuk ki.) Rajzoljunk rá egy
egyenest, ez lesz a tengely, és jelöljünk ki egy a tengelyre nem
illeszkedő pontot! Hajtsuk félbe a lapot a tengely mentén, és szúrjuk ki a
képét.
F2 .:
Vizsgáld meg, hogy a tengelyre nem eső pont és tükörképe hogyan
helyezkedik el a tengelyhez képest!
2. A tengelyre nem illeszkedő pontokra teljesül,
hogy a pontot és a tükörképét összekötő szakasznak a tengely
felezőmerőlegese.
A tengely bármely pontjától a tárgypont és a képpont egyenlő távol van. (Ha idegenkedünk a „tárgypont – képpont” kifejezésektől, akkor fogalmazzuk így: a pont és a tükörképe!)
A tengely bármely pontjától a tárgypont és a képpont egyenlő távol van. (Ha idegenkedünk a „tárgypont – képpont” kifejezésektől, akkor fogalmazzuk így: a pont és a tükörképe!)
F3
– F7 .: Maca
tükörképeket alkotott, bizony nem túl ügyesen. Keresd a hibákat, és fogalmazd
meg milyen törvényszerűségek ellen vétett Maca az egyes esetekben!
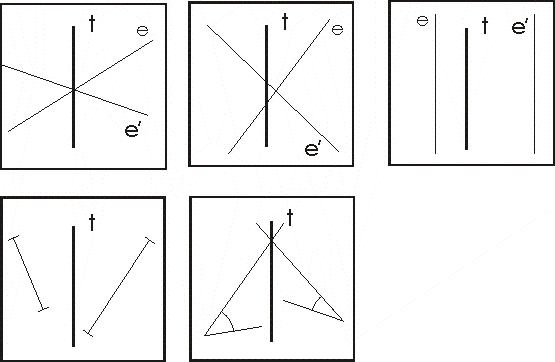
3. A tengelyt metsző egyenes és a képe a tengellyel
egyenlő szöget zár be.
4. A tengelyt metsző egyenes képe a tengelyt ugyanabban a pontban metszi.
5. A tengellyel párhuzamos egyenes képe is párhuzamos a tengellyel, ugyanolyan messze van attól, annak túloldalán. Ekkor az eredeti és a képegyenes középpárhuzamosa a tengely.
Van-e olyan egyenes is, amelyik nem „kettőződik meg” a tükrözés hatására, azaz a tükörképe önmaga?
Igen. A tengelyre merőlegesek és a tengely.
Mi a kettő közötti különbség?
A merőlegesek „megfordulnak”, csak a tengellyel közös pontjuk marad helyben, míg a tengelynek minden pontja helyben marad.
6. Szakasz és a képe egyenlő hosszú.
7. Szög és a képe egyenlő nagyságú.
4. A tengelyt metsző egyenes képe a tengelyt ugyanabban a pontban metszi.
5. A tengellyel párhuzamos egyenes képe is párhuzamos a tengellyel, ugyanolyan messze van attól, annak túloldalán. Ekkor az eredeti és a képegyenes középpárhuzamosa a tengely.
Van-e olyan egyenes is, amelyik nem „kettőződik meg” a tükrözés hatására, azaz a tükörképe önmaga?
Igen. A tengelyre merőlegesek és a tengely.
Mi a kettő közötti különbség?
A merőlegesek „megfordulnak”, csak a tengellyel közös pontjuk marad helyben, míg a tengelynek minden pontja helyben marad.
6. Szakasz és a képe egyenlő hosszú.
7. Szög és a képe egyenlő nagyságú.
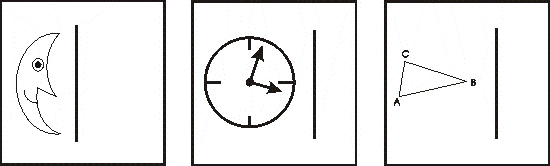
F8.:
Készítsd el
másolópapíron mindhárom ábrát a tükörképükkel együtt. Fogalmazd meg, amit
észrevettél!
M.: E
feladat megbeszélése során hallhatunk majd kedves próbálkozásokat a körüljárási
irány fogalmának megragadására. Most áruljuk tehát el, hogy ezt így nevezik.
Ezután várjuk a megfogalmazást a megfelelő új kifejezés alkalmazásával.
8. Alakzat és tükörképe fordított
körüljárású. (A tengelyes tükrözés a körüljárási irányt megfordítja.)
M.: Módszertani
gyakorlaton (tanárképző főiskolásoknak) otthoni feladatként szoktam
adni, hogy a tengelyes tükrözés tulajdonságainak „felfedeztetésére” dolgozzanak
ki kísérlet sorozatot. Szebbnél szebb ötletek születnek, ami mutatja, hogy
korántsem egyetlen és üdvözítő mód az itt leírt. Csupán szellemében hiszek
rendíthetetlenül, mert eddigi gyakorlatomban azt látom, hogy az ilyen úton
szerzett tudás értelmes tudás és maradandó.
További hozadéka még, hogy az állandó fogalmaztatás aktív nyelvhasználatot kényszerít, ezzel segíti, hogy tanítványaink 4 év alatt szabatos, pontos, jól felépített érvelések megalkotására váljanak képessé.
További hozadéka még, hogy az állandó fogalmaztatás aktív nyelvhasználatot kényszerít, ezzel segíti, hogy tanítványaink 4 év alatt szabatos, pontos, jól felépített érvelések megalkotására váljanak képessé.