| Szerkesztési feladatok |
| Területátalakítások |
| Szabályos sokszögek |
| Pitagorasz tétele |
| Tengelyes tükrözés |
| Középpontos tükrözés |
| Forgatás |
| Eltolás |
| Szélsőérték-feladatok (Markó Gábor munkája) |
|
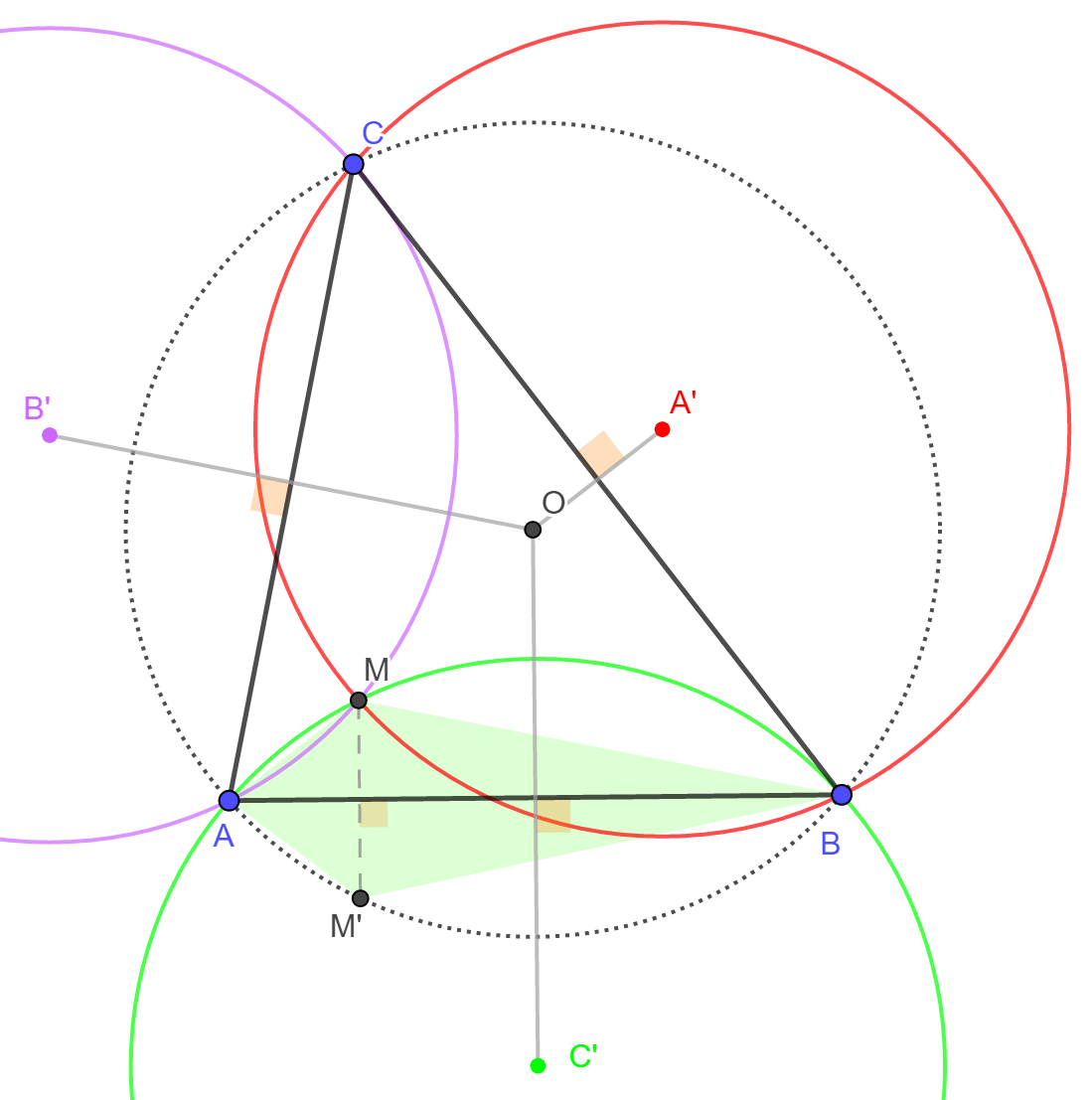
A hegyesszögű ABC háromszög magasságpontja M. A BCM, CAM, ABM háromszögek köré írt kör középpontja rendre A', B' és C'.
|
|
A BCM, CAM és ABM háromszögek köré írt körök sugara megegyezik egymással, továbbá megegyezik az ABC háromszög köré írt kör sugarával is. Ennél többet mutatunk meg: a BCM, CAM, ABM háromszögek körülírt köre épp az ABC háromszög köré írt kör tükörképe az ABC háromszög megfelelő oldalegyenesére vonatkozóan. Ennek igazolásához felhasználjuk, hogy a hegyesszögű háromszög magasságpontjának bármely oldalegyenesre vonatkozó tükörképe illeszkedik a háromszög köré írt körre. Ha tehát az ABC háromszög M magasságpontját tükrözzük az AB egyenesre, akkor a kapott M' pont rajta van a körülírt körön. Ha most az ABM háromszöget is tükrözzük, akkor képként az ABM' háromszöget kapjuk, és így az ABM' háromszög köré írt kör megegyezik az ABC háromszög köré írt körrel. Ebből már következik, hogy az ABM háromszög és az ABC háromszög köré írt kör AB egyensre vonatkozó tükörképe megegyeznek. A C' pont pedig megegyezik az ABC háromszög köré írt kör O középpontjának AB egyenesre vonatkozó tükörképével. Hasonló állítás igazolható a B', C' pontokra is.
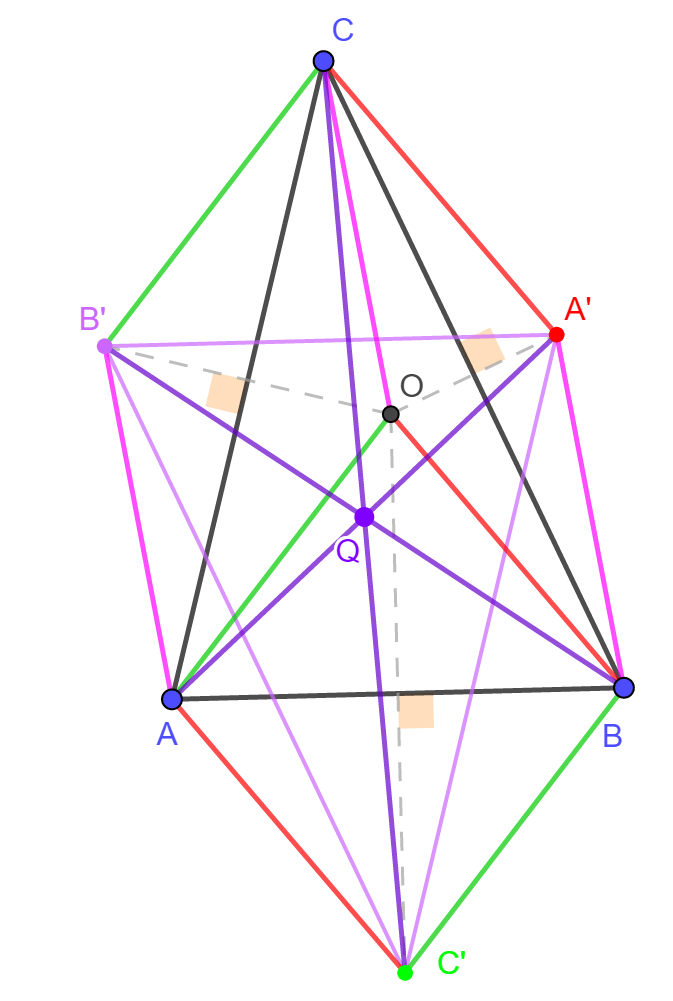
Vizsgáljuk most az AA', BB', CC' szakaszokat, valamint az A'B'C' háromszöget az alábbi ábra segítésgével! Eredményeink alapján az OAC'B négyszög átlói merőlegesen felzik egymást, ezért a négyszög rombusz. Ezt akár úgy is beláthatjuk, hogy OA=OB (ABC háromszög köré írt kör sugarai), a tükrözés miatt pedig OA=C'A és OB=C'B, ezért a négyszög minden oldala egyenlő, így valóban rombuszról van szó. Ebből következően AC' és OB párhuzamosak és egyenlő hosszúak. Ugyanígy látható be, hogy OBA'C is rombusz, ezért az OB szakasz CA'-vel is párhuzamos és egyenlő hosszú. Így AC' és CA' párhuzamosak és egyenlők (az ábrán piros szakaszok), ezért AC'A'C parelelogramma. Ebből persze azonnal következik, hogy CA és A'C' is párhuzamos és egyenlő, továbbá hogy az AA' és CC' átlók felezik egymást. Ugyanez a gondolatmenet arra is alkalmas, hogy az ABA'B' négyszögről mutassuk meg, hogy paralelogramma, amiből adódik, hogy A'B' párhuzamos és egyenlő AB-vel, továbbá a BB' átló is felezi az AA' átlót. Végül paralelogramma a BCB'C' négyszög is, így BC párhuzamos és egyenlő B'C'-vel. Összefoglalva az eddigieket: az ABC és az A'B'C' háromszögek oldalai páronként párhuzamosak és egyenlők, azaz a két háromszög egybevágó egymással, továbbá az AA', BB', CC' szakaszok egy pontban (Q) felezve metszik egymást. A Q-ra vonatkozó középpontos tükrözés az ABC és A'B'C' háromszögeket egymásba viszi át.
|