Határozza meg az $n$ természetes számot és az $X$ számjegyet, ha teljesül, hogy

$  \dfrac{n}{1221}=0,\dot{1}2\dot{X} = 0, 12X12X12X\ldots  $

Megtekintés helyben: 

   

Megtekintés új oldalon: 

        

Feladatlapba

Határozza meg a $p$ valós paraméter azon értékeit, amelyekre a következő egyenletnek nincs megoldása a valós számok halmazán:

$ 500\cdot 25^{x}= 10^{2x+3} \cdot 2^{x^2-p} $

Megtekintés helyben: 

   

Megtekintés új oldalon: 

        

Feladatlapba

Nevezzük a $H$ számot "hatszögletű-kerekerdő-szám"-nak, ha a szabályos háromszögrács egy szabályos hatszögének  belsejében és határán összesen pontosan $H$ darab rácspont van. Jelölje $h_n$ a nagyság szerinti sorrendben az "$n$"-edik "hatszögletű-kerekerdő-szám"-ot. Az alábbi ábra az első három "hatszögletű-kerekerdő-szám"-ot szemlélteti ( $h_1 = 1,\ h_2 = 7,\ h_3 = 19$).

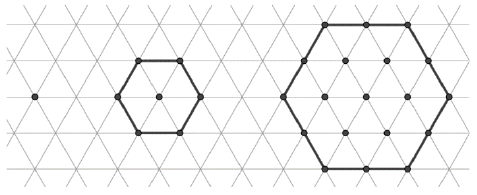
a) Határozza meg $ h_5 $ értékét.

b) Adja meg $ h_n$ értékét n függvényében.

c) Adja meg az összes olyan "hatszögletű-kerekerdő-szám"-okból álló számpárt, amelyek különbsége 60.

Megtekintés helyben: 

   

Megtekintés új oldalon: 

        

Feladatlapba

Legyen az $ ABC $ derékszögű háromszög $ AB $ átfogójának felezőpontja $ D $, továbbá az $ E $ az $ AC $, az $ F $ pedig a $ BC $ befogó egy-egy belső pontja úgy, hogy $ EDF\sphericalangle = 90^\circ $ teljesül. Bizonyítsa be, hogy $ EF = AE^2 + BF^ 2 $ .

Megtekintés helyben: 

   

Megtekintés új oldalon: 

        

Feladatlapba

Legyenek $ a $, $ b $ és $ c $ olyan pozitív valós számok, amelyekre $ a + b + c = 1 $.

a) Bizonyítsa be, hogy

$ \dfrac{4}{3}\le ( a + b )^2 + ( b + c )^2 + ( c + a )^2  $

Az $ a $, $ b $ és $ c $ mely értékei esetén teljesül az egyenlőség?

b) Igazolja, hogy

$ ( a + b )^2 + ( b + c )^2 + ( c + a )^2 < 2. $

Megtekintés helyben: 

   

Megtekintés új oldalon: 

        

Feladatlapba