Nevezzük a $H$ számot "hatszögletű-kerekerdő-szám"-nak, ha a szabályos háromszögrács egy szabályos hatszögének  belsejében és határán összesen pontosan $H$ darab rácspont van. Jelölje $h_n$ a nagyság szerinti sorrendben az "$n$"-edik "hatszögletű-kerekerdő-szám"-ot. Az alábbi ábra az első három "hatszögletű-kerekerdő-szám"-ot szemlélteti ( $h_1 = 1,\ h_2 = 7,\ h_3 = 19$).

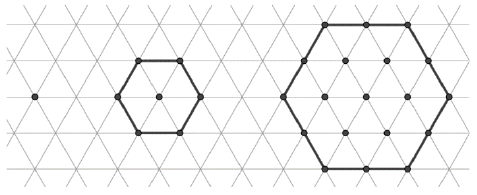
a) Határozza meg $ h_5 $ értékét.

b) Adja meg $ h_n$ értékét n függvényében.

c) Adja meg az összes olyan "hatszögletű-kerekerdő-szám"-okból álló számpárt, amelyek különbsége 60.

Megoldás: 

$ h_ 5 $ és $ h_1$

$  h_{11} $ és $ h_{10} $