Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium
Látogatók
Összes:
9 223 861
Mai:
4 738
216.73.216.221
(IP: 216.73.216.221)
|
1. találat: OKTV 20182019 I. kategória 1. forduló 1. feladat
Témakör: *Számelmélet (Azonosító: OKTV_20182019_1k1f1f )
A tízes számrendszerben felírt $ x $ pozitív egész szám számjegyeinek összege 7, a számjegyek szorzata 6, és az $ x $ szám osztható 16-tal. Határozza meg az összes ilyen számot.
*Kombinatorika ( oszthatóság) (Azonosító: OKTV_20182019_1k1f2f )
Hányféle módon állítható elő a $ 2018 $ legalább két egymást követő pozitív egész szám összegeként?
*Kombinatorika ( oszthatóság) (Azonosító: OKTV_20182019_1k1f3f )
Egy ládában megromlott a benne levő almák egy része. Eltávolítunk 10 hibás almát, így annak a valószínűsége, hogy a maradékból véletlenszerűen kivéve egy almát, az hibás lesz, felére csökken az eredetihez képest. Ezután még 5 hibás almát kiveszünk. Ezzel annak a valószínűsége, hogy a maradékból véletlenszerűen egyet kivéve, a kivett alma hibás lesz, az egyötödére csökken az eredeti állapothoz képest. Hány jó alma volt a ládában?
*Geometria (Azonosító: OKTV_20182019_1k1f4f )
Az $ ABCD $ húrnégyszög $ AC $ átlója a húrnégyszög körülírt körének átmérője. Bizonyítsa be, hogy a négyszög szemközti oldalainak a $ BD $átlóra eső merőlegesvetületei egyenlő hosszúak.
*Kombinatorika (Azonosító: OKTV_20182019_1k1f5f )
A mellékelt ábra szerinti táblán korongokkal játszunk. Induláskor 3 korong van a táblán, a rajzon ezeket a nagyobb körök jelzik. Két pont szomszédos, ha él köti össze őket. A tábla szabad pontjaiba egyenként további korongokat akarunk helyezni úgy, hogy ha a feltett korongnak van közvetlen szomszédja (egy vagy több), akkor a szomszédok közül pontosan egyet kötelező levenni. A játék folyamán mennyi lehet a táblán lévő korongok a) minimális száma? b) maximális száma? c) Adjon meg egy eljárást a maximális érték eléréséhez. 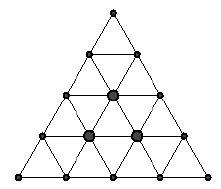
*Geometria (Azonosító: OKTV_20182019_1k1f6f )
Az $ ABCD $ trapéz párhuzamos oldalai $ AB $ és $ CD, $ amelyekre $ AB > CD, $ továbbá teljesül, hogy a trapéz $ AD $ szára merőleges $ AB $-re. Az $ AD $ szár, mint átmérő fölé szerkesztett kör a $ BC $ szárat érinti. Jelöljük a trapéz átlóinak metszéspontját $ E $-vel és húzzunk az $ E $ ponton át párhuzamost az $ AB $ oldallal, ez az egyenes a $ BC $ szárat az $ F $ pontban metszi. Az $ AD $ szár felezőpontját $ O $-val jelöljük. Bizonyítsa be, hogy $ AF || C $ és $ OF \perp BC. $
|
|
Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium
|
QR kód
Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium

|
|
Bejelentkezés cikkíróknak
|
|


