Feladatbank keresés

Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium

Látogatók

Összes:

7 597 266

Mai:

4 430

18-97-9-168.crawl.commoncrawl.org
(IP: 18.97.9.168)

Honlapok

SULINET Matematika

Oktatási Hivatal

Versenyvizsga portál

Matematika Portálok

Berzsenyi Dániel Gimnázium

Óbudai Árpád Gimnázium

Szent István Gimnázium

Békásmegyeri Veres Péter Gimnázium

Első lap
1
Utolso lap

Találatok száma: 6 (listázott találatok: 1 ... 6)

1. találat: OKTV 2014/2015 I. kategória 1. forduló 1. feladat
Témakör: *Számelmélet (algebra, oszthatóság) (Azonosító: OKTV_20142015_1k1f1f )

Határozza meg a tízes számrendszerbeli $x=\overline{abba}$ és $y=\overline{abab}$ $(a \ne b)$ páros természetes számokat úgy, hogy az $x+y$összeg osztható legyen 7-tel.

Megtekintés helyben:

Megtekintés új oldalon:

Feladatlapba

2. találat: OKTV 2014/2015 I. kategória 1. forduló 2. feladat
Témakör: *Geometria (párhuzamos szelőszakaszok) (Azonosító: OKTV_20142015_1k1f2f )

Az AF, CE és BD szakaszok az alábbi ábrának megfelelőenhelyezkednek el. A CE szakasz hossza 24, a BD szakasz hossza 40 egységnyi. Hány egység hosszúságú az AF szakasz? 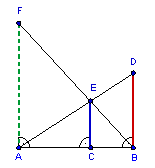oktv1415 1kat 1ford f2 001

Megtekintés helyben:

Megtekintés új oldalon:

Feladatlapba

3. találat: OKTV 2014/2015 I. kategória 1. forduló 3. feladat
Témakör: *Algebra (oszthatóság) (Azonosító: OKTV_20142015_1k1f3f )

Oldja meg az

$x^2+y^2-8z=14$

egyenletet az egész számok halmazán.

Megtekintés helyben:

Megtekintés új oldalon:

Feladatlapba

4. találat: OKTV 2014/2015 I. kategória 1. forduló 4. feladat
Témakör: *Algebra (logaritmus) (Azonosító: OKTV_20142015_1k1f4f )

Oldja meg a valós számok halmazán az

$log_5(x+4)\cdot log_5(x-1)=log_5\left ( (x+4)^2 \cdot (x-1) \right )-2$

egyenletet!

Megtekintés helyben:

Megtekintés új oldalon:

Feladatlapba

5. találat: OKTV 2014/2015 I. kategória 1. forduló 5. feladat
Témakör: *Geometria (kerületi-középponti szögek) (Azonosító: OKTV_20142015_1k1f5f )

Az ABCD húrnégyszög BC és AD oldalainak egyenesei a hegyesszögű CDE háromszöget zárják közre. A CDE háromszög körülírt körének sugara megegyezik az ABCD húrnégyszög körülírt körének sugarával.
Bizonyítsa be, hogy $\dfrac{AB}{CD}=2\cdot cos(CED\angle )$!

Megtekintés helyben:

Megtekintés új oldalon:

Feladatlapba

6. találat: OKTV 2014/2015 I. kategória 1. forduló 6. feladat
Témakör: *Logika (táblázat) (Azonosító: OKTV_20142015_1k1f6f )

Hányféleképpen írhatjuk be az ábrán látható négyzetekbe az 1; 2; 3; 4; 5; 6 számokat úgy,

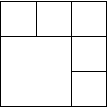oktv1415 1kat 1ford f6 001 hogy a szomszédos négyzetekbe írt számok különbsége ne legyen 3? (Szomszédosnak tekintünk két négyzetet, ha van közös oldaluk.)