Adott a $ [–2; 4]$ zárt intervallumon értelmezett $f$ függvény: $x \rightarrow -\dfrac{1}{2} x + 4$

a) Mit rendel az $f$ függvény az $x = -\dfrac{3}{4}$ számhoz?

b) Ábrázolja az $f$ grafikonját! Adja meg az $f$ értékkészletét!

Adott a valós számok halmazán értelmezett $g$ függvény: $x \rightarrow x^2 - 4 x + 3$

c) Hány olyan szám van, amelyhez a $g$ függvény a $ \left( -\dfrac{3}{4}\right)$ értéket rendeli?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

A statisztikai adatok szerint a közúti balesetek gyakori okai között minden évben szerepel a járművezetők figyelmetlensége, a gondatlan vezetés.

a) Egy autó az autópályán 120 km/h sebességgel halad, és a sofőr 1,5 másodpercig nem figyel az útra. Hány métert tesz meg az autó ennyi idő alatt?

A gyorshajtás szintén a gyakori baleseti okok között szerepel. A tapasztalatok szerint, ha egy sofőr betartja az autópályán a 130 km/h sebességhatárt, akkor az átlagsebessége legfeljebb 120 km/h körül alakulhat. A Siófok–Budapest távolság közelítőleg 100 km.

b) Számítsa ki, hogy hány perccel rövidebb idő szükséges a Siófok–Budapest távolság megtételéhez, ha 120 km/h átlagsebesség helyett átlagosan 130 km/h-val teszi meg ezt a távot egy autó!

2018 januárjában Magyarországon összesen 1178 személyi sérüléssel járó közúti baleset történt, melyek közül 440 esetben a gyorshajtás volt a fő ok. A balesetek okainak meg- oszlását egy kördiagramon szeretnénk ábrázolni.

c) Mekkora középponti szög tartozik a kördiagramon a gyorshajtáshoz? Válaszát egész fokra kerekítve adja meg!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

a) Egy számtani sorozat első és harmadik tagjának összege 8. A sorozat harmadik, negyedik és ötödik tagjának összege 9. Adja meg a sorozat első tíz tagjának összegét!

b) Egy derékszögű háromszög egyik befogója 8 cm-rel, a másik 9 cm-rel rövidebb, mint az átfogó. Mekkorák a háromszög oldalai?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Egy A4-es papírlapot négy egyforma kisebb lapra vágtunk. Ezekre a kisebb lapokra felírtuk az 1, 2, 3, 4 számokat, mindegyik lapra egy számot. A négy lapot véletlenszerűen sorba rakjuk.

a) Mennyi annak a valószínűsége, hogy így sem két páros, sem két páratlan szám nem kerül egymás mellé?

Egy A4-es papírlap vastagsága 0,1 mm. Egy ilyen papírlapot kettévágunk, majd a keletkező két fél lapot egymásra tesszük. Az így kapott "kupacot" ismét kettévágjuk, és a keletkező négy negyedlapot egymásra tesszük (a kupac magassága ekkor 0,4 mm). Ezt a műveletet tovább folytatjuk, tehát először egy vágással a kupacot kettévágjuk, majd a keletkező lapokat egymásra tesszük. Azt tervezzük, hogy ezt a műveletet összesen 20-szor hajtjuk végre. Luca szerint, ha ezt meg tudnánk tenni, akkor a 20 vágás és egymásra rakás után keletkező kupac magasabb lenne, mint 100 méter.

b) Igaza van-e Lucának? Válaszát számítással igazolja!

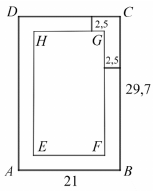
Egy A4-es papírlap méretei: 21 cm x 29,7 cm. A szövegszerkesztő programok általában 2,5 cm-es margóval dolgoznak, vagyis a papírlap minden oldalától számítva egy-egy 2,5 cm-es sáv üresen marad (lásd az ábrát). A lap közepén a szövegnek fennmaradó rész szintén téglalap alakú. Zsófi szerint az ABCD és az EFGH téglalapok hasonlók.

c) Igaza van-e Zsófinak? Válaszát indokolja!

Tekintsük a következő állítást:

Ha két négyszög hasonló, akkor megfelelő szögeik páronként egyenlők.

d)Adja meg az állítás logikai értékét (igaz vagy hamis)! Írja fel az állítás megfordítását, és adja meg a megfordítás logikai értékét is! Ez utóbbi válaszát indokolja!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Az $ABCDEFGH$ kocka élhosszúsága 6 cm.

a) Számítsa ki az ábrán látható $ABCDE$ gúla felszínét!

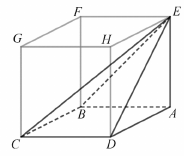b) Fejezze ki az $\overrightarrow{EC}$ vektort az $\overrightarrow{AB}$ , az $\overrightarrow{AD}$ és az $\overrightarrow{AE}$ vektorok segítségével!

Egy 12 cm magas forgáskúp alapkörének sugara 6 cm.

c) Mekkora szöget zár be a kúp alkotója az alaplappal?

A fenti forgáskúpot két részre vágjuk az alaplap síkjával párhuzamos síkkal. Az alaplap és a párhuzamos sík távolsága 3 cm.

d) Számítsa ki a keletkező csonkakúp térfogatát!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Egy 125 férőhelyes szállodában összesen 65 szoba van: egy-, két- és háromágyasak.

a) Hány háromágyas szoba van a szállodában, ha a kétágyas szobák száma háromszorosa az egyágyas szobák számának?

A szállodába egy hat főből álló társaság érkezik: Aladár, Balázs, Csaba, Dezső, Elemér és Ferenc. Aladár és Balázs testvérek. A társaság tagjai az egyágyas 101-es, a kétágyas 102-es és a háromágyas 103-as szobát kapják. A recepciós kitesz a pultra egy darab 101-es, két darab 102-es és három darab 103-as szobakulcsot. A társaság tagjai a pultra helyezett kulcsok közül véletlenszerűen elvesznek egyet-egyet (ezzel kiválasztják a szobájukat).

b) Határozza meg annak a valószínűségét, hogy Aladár és Balázs kerül a 102-es szobába!

Érkezésük után a vendégek a szálloda éttermében vacsoráztak. Vacsorájukra várva látták, hogy az egyik pincér – sietős mozdulatai közben – leejtett és összetört egy tányért. A szálloda pincérei felszolgálás közben átlagosan minden kétezredik tányért összetörik (ezt tekinthetjük úgy, hogy $\dfrac{1}{2000}$ annak a valószínűsége, hogy egy adott tányért összetörnek). A pincérek a következő vacsora alkalmával összesen 150 tányért szolgálnak fel.

c) Határozza meg annak a valószínűségét, hogy a következő vacsora közben a pincérek legalább egy tányért összetörnek!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba