Az $ABCDEFGH$ kocka élhosszúsága 6 cm.

a) Számítsa ki az ábrán látható $ABCDE$ gúla felszínét!

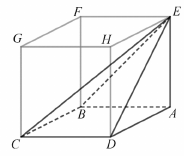b) Fejezze ki az $\overrightarrow{EC}$ vektort az $\overrightarrow{AB}$ , az $\overrightarrow{AD}$ és az $\overrightarrow{AE}$ vektorok segítségével!

Egy 12 cm magas forgáskúp alapkörének sugara 6 cm.

c) Mekkora szöget zár be a kúp alkotója az alaplappal?

A fenti forgáskúpot két részre vágjuk az alaplap síkjával párhuzamos síkkal. Az alaplap és a párhuzamos sík távolsága 3 cm.

d) Számítsa ki a keletkező csonkakúp térfogatát!

 Megoldás:

a.) $ 36 + 2 \cdot 18 + 2 \cdot 18 \cdot \sqrt{ 2 } \approx 122,9\ cm^2$

b.) $\overrightarrow{EC} = - \overrightarrow{AE} + \overrightarrow{AD} + \overrightarrow{AB}$

c.) $ \approx 63,4^\circ$
d.) $ 83,25\pi\ cm^3 \approx 261,5 cm^3$