(Feladat azonosítója: mmk_201910_2r16f )
Témakör: *Geometria
Egy A4-es papírlapot négy egyforma kisebb lapra vágtunk. Ezekre a kisebb lapokra felírtuk az 1, 2, 3, 4 számokat, mindegyik lapra egy számot. A négy lapot véletlenszerűen sorba rakjuk.
a) Mennyi annak a valószínűsége, hogy így sem két páros, sem két páratlan szám nem kerül egymás mellé?
Egy A4-es papírlap vastagsága 0,1 mm. Egy ilyen papírlapot kettévágunk, majd a keletkező két fél lapot egymásra tesszük. Az így kapott "kupacot" ismét kettévágjuk, és a keletkező négy negyedlapot egymásra tesszük (a kupac magassága ekkor 0,4 mm). Ezt a műveletet tovább folytatjuk, tehát először egy vágással a kupacot kettévágjuk, majd a keletkező lapokat egymásra tesszük. Azt tervezzük, hogy ezt a műveletet összesen 20-szor hajtjuk végre. Luca szerint, ha ezt meg tudnánk tenni, akkor a 20 vágás és egymásra rakás után keletkező kupac magasabb lenne, mint 100 méter.
b) Igaza van-e Lucának? Válaszát számítással igazolja!
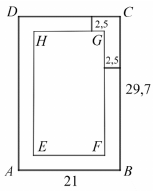
Egy A4-es papírlap méretei: 21 cm x 29,7 cm. A szövegszerkesztő programok általában 2,5 cm-es margóval dolgoznak, vagyis a papírlap minden oldalától számítva egy-egy 2,5 cm-es sáv üresen marad (lásd az ábrát). A lap közepén a szövegnek fennmaradó rész szintén téglalap alakú. Zsófi szerint az ABCD és az EFGH téglalapok hasonlók.
c) Igaza van-e Zsófinak? Válaszát indokolja!
 Tekintsük a következő állítást:
Tekintsük a következő állítást:
Ha két négyszög hasonló, akkor megfelelő szögeik páronként egyenlők.
d)Adja meg az állítás logikai értékét (igaz vagy hamis)! Írja fel az állítás megfordítását, és adja meg a megfordítás logikai értékét is! Ez utóbbi válaszát indokolja!
Megoldás:
a.) $ P=\dfrac{1}{3}$
b.) Lucának tehát igaza van.
c.) Zsófinak nincs igaza.
d.) Az állítás igaz. A megfordítása nem.