a) Oldja meg az alábbi egyenletet a valós számok halmazán!

$ (2^x - 3)^2 = 2^ {x+1} + 9 $

Legyen $ f ( x) = x^2 - 9 x + 14 $ , ahol x valós szám.
Tekintsük a következő állítást: „Ha $ x > 7 $, akkor $ f (x) > 0 $.”
b) Adja meg az állítás logikai értékét (igaz vagy hamis)! Válaszát indokolja!
c) Fogalmazza meg az állítás megfordítását! Igaz-e az állítás megfordítása? Válaszát indokolja!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Margiték autójában a fedélzeti számítógép kiszámítja, hogy az autó üzemanyagtartályában lévő benzin még hány kilométer megtételéhez elegendő. Nevezzük ezt hátralévő távolságnak. A számításhoz a gép a legutolsó tankolás óta mért átlagos fogyasztást veszi alapul, és úgy számol, hogy az autó a jövőben is ezzel az átlagfogyasztással fog haladni. A legutóbbi tankolás alkalmával teletöltötték az autó üzemanyagtartályát, így 45 liter benzin volt benne. A tankolás óta éppen 200 kilométert tettek meg a városban, ekkor az autó átlagfogyasztása 10 liter volt 100 kilométerenként.
a) Számítsa ki a városi autózás után a hátralévő távolságot!
A 200 kilométeres városi autóhasználatot követően Margiték egynapos autós kirándulást tettek vidéken, ezalatt összesen 100 kilométert autóztak (újabb tankolás nélkül). A kirándulás végén a kijelző alapján 200 kilométerre elegendő benzin maradt, azaz ennyi lett a hátralévő távolság.
b) Mennyi volt az autó 100 km-re vonatkozó átlagfogyasztása a kirándulás során?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

a)Hány olyan pozitív háromjegyű szám van a tízes számrendszerben, amely a 8 és a 9 számok közül legalább az egyikkel osztható?
b) A 8-as számrendszerben háromjegyű pozitív egész számok közül véletlenszerűen kiválasztunk egyet. Mennyi a valószínűsége annak, hogy a kiválasztott szám a 9-es számrendszerben is háromjegyű?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Egy többnapos nemzetközi matematikakonferencia minden résztvevője belépőkártyát kap, amelyen a PQRST konvex ötszög és annak átlói láthatók.

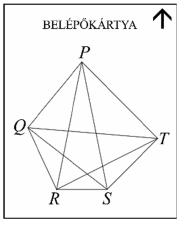A szervezők úgy tervezik, hogy egy-egy belépőkártyán az ötszög oldalai és átlói közül valahányat (egyet vagy többet, akár az összeset, de az is lehet, hogy egyet sem) megvastagítanak, így a különböző személyek különböző ábrájú kártyát kapnak. Az elektronikus kapu optikai leolvasója ez alapján engedélyezi a belépést, és elvégzi a személy regisztrációját. (Két belépőkártya különböző, ha az egyiken szerepel olyan megvastagított szakasz, amelyik a másikon nem.) A konferenciának 400 résztvevője lesz.

a) Jut-e mindenkinek különböző belépőkártya?
A konferencia épülete egy háromszög alakú területen van. Ha a háromszög csúcsai $ A $, $ B $ és $ C $, akkor $ AB = AC = 130 $ méter, és $ BC $ = 100 méter. A háromszög alakú területet kettéosztja az egyenes $ CD $ kerítés úgy, hogy a $ BCD $ háromszög alakú rész területe $ 2000 m^2 $. 

b) Milyen hosszú a CD kerítés?
A konferencián 200 magyar, 70 angol és 130 német matematikus vesz részt. Az angolok életkorának átlaga 44 év, a németeké 48 év, az összes résztvevő életkorának átlaga 45,7 év.
c) Mennyi a magyar résztvevők életkorának átlaga?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba