Adott két függvény: $ f : ] 0;130 [ \rightarrow \mathbb{R} ;\  f ( x) = 900 - 0,25( x - 60)^2 $, illetve $ g : ]0;130[ \rightarrow \mathbb{R};\ g ( x ) = 6,4 x $ .
a) Adja meg az $ f$  zérushelyét!
b) Számítsa ki az $ f(20) - g(20) $ különbség értékét!
c) Adja meg a $ h : ] 0;130 [ \rightarrow \mathbb{R};\ h ( x) = f ( x ) - g ( x) $függvény szélsőértékét (típusát,
helyét és értékét)!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Egy továbbképzésen részt vevő csoport tagjai életkorának átlaga 28 év. Az öt legidősebb résztvevő életkorának átlaga 40 év, a többieké 25,6 év.
a) Hány nő és hány férfi vesz részt a továbbképzésen, ha 1,5-szer annyi nő van a csoportban, mint férfi?
A csoport tagjai az egyik napon "keleties" ebédet kaptak. Az ételek ízesítéséhez hatféle fűszer állt rendelkezésükre: keserű, savanyú, édes, sós, csípős és fanyar.
b) Hányféleképpen ízesíthetik az ételeiket a résztvevők úgy, hogy a hatból három- vagy négyféle fűszert használhatnak, de az édes és a keserű nem szerepelhet egyszerre?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Van néhány dobozunk és valahány érménk. Ha minden dobozba egy érmét teszünk, akkor m darab érme kimarad. Ha minden dobozba pontosan m db érmét akarunk tenni, akkor m dobozba nem jut érme (m ≠ 1).
a) Hány érménk lehet, ha a dobozok száma 6?
Egy dobozban több ezer érme van, amelyek 3%-a hibás. Az érmék közül véletlenszerűen kiválasztunk 80-at. (Az érmék nagy száma és az alacsony hibaszázalék miatt a kiválasztás visszatevéses mintavétellel is modellezhető.)
b) Mennyi annak a valószínűsége, hogy legfeljebb 2 hibás érme lesz a kiválasztott érmék között?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Ha András az asztalra ejti a pingponglabdáját, akkor a labda az ejtési magasság kb. 84%-ára pattan vissza. Ezután tovább pattog úgy, hogy minden asztalra érkezés után az előző felpattanás magasságának 84%-áig emelkedik fel.
a) András egy alkalommal (az asztal lapjától mérve) 1 méter magasságból ejtette az asztalra a ingponglabdát. Mekkora utat tesz meg összesen a pingponglabda az első asztalra érkezésétől a tizenötödikig? (Feltételezzük, hogy a labda csak függőleges irányban mozog, a vízszintes irányú elmozdulása elhanyagolható.) András azt állítja, hogy az összes pingponglabdájának száma 6-tal osztva 2 maradékot, 15-tel osztva pedig 1 maradékot ad.
b) Mutassa meg, hogy András állítása hamis!
Dóri olyan pingponglabda-készletet vásárolt, amelynek dobozába három egyforma labda – az ábrán látható elrendezésben – szorosan belefér. A doboz hengeres test, melynek alaplapját három egybevágó körív és három egyenlő hosszúságú szakasz határolja. (Az ábrán a dobozt felülnézetből látjuk.)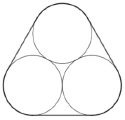

c) A doboz térfogatának hány százalékát tölti ki a három pingponglabda, ha a labdák átmérője 40 mm? (A doboz falvastagsága elhanyagolható.)

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba