Ha András az asztalra ejti a pingponglabdáját, akkor a labda az ejtési magasság kb. 84%-ára pattan vissza. Ezután tovább pattog úgy, hogy minden asztalra érkezés után az előző felpattanás magasságának 84%-áig emelkedik fel.
a) András egy alkalommal (az asztal lapjától mérve) 1 méter magasságból ejtette az asztalra a ingponglabdát. Mekkora utat tesz meg összesen a pingponglabda az első asztalra érkezésétől a tizenötödikig? (Feltételezzük, hogy a labda csak függőleges irányban mozog, a vízszintes irányú elmozdulása elhanyagolható.) András azt állítja, hogy az összes pingponglabdájának száma 6-tal osztva 2 maradékot, 15-tel osztva pedig 1 maradékot ad.
b) Mutassa meg, hogy András állítása hamis!
Dóri olyan pingponglabda-készletet vásárolt, amelynek dobozába három egyforma labda – az ábrán látható elrendezésben – szorosan belefér. A doboz hengeres test, melynek alaplapját három egybevágó körív és három egyenlő hosszúságú szakasz határolja. (Az ábrán a dobozt felülnézetből látjuk.)

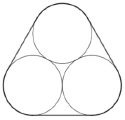
c) A doboz térfogatának hány százalékát tölti ki a három pingponglabda, ha a labdák átmérője 40 mm? (A doboz falvastagsága elhanyagolható.)

Megoldás:

a) $ \approx  9,59 m $

b) Igaz az állítás (András hamisat állít)

c) $ \approx  58\%$