a) Egy mértani sorozat hányadosa $ \dfrac{1}{ 4} $, a sorozat első öt tagjának összege $ 852,5 $. Határozza meg a sorozat első tagját! Számításai során ne használjon közelítő értéket!

b) Egy számtani sorozat első öt tagjának összege $ 852,5 $; első tíz tagjának összege pedig $ 2330 $. Számítsa ki a sorozat első tagját és differenciáját!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

a) Oldja meg az alábbi egyenletet a valós számok halmazán!

$ 25\cdot\left( \dfrac{1}{5} \right)^x-50\cdot\left( \dfrac{1}{5} \right)^{x+1}+30\cdot\left( \dfrac{1}{5} \right)^{x+2}=81$

b) Igazolja, hogy $\dfrac{\lg 5^x+\lg 5^{-x}}{2}\le \lg \dfrac{5^x+5^{-x}}{2}\ (x\in\mathbb{R}) $

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Egy nagy méretű, köztéren felállítandó óra számlapját szabályos 12-szög alakúra tervezik. Az $ A_1A_2\ldots A_{12} $ számlapot egy $ 260 cm \times 180 cm $-es téglalap alakú alumíniumlemezből vágják ki az ábra szerint.

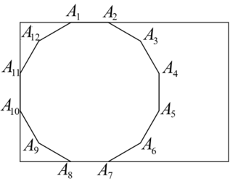
a) Mekkora tömegű az óralap, ha az alumíniumlemez vastagsága $ 2 mm $, és $ 1 m^3 $ alumínium tömege 2700 kg?

b) Jelöljük meg a szabályos tizenkétszög $ A_1 $ csúcsát! Hány olyan derékszögű háromszög van, amelynek egyik csúcsa az $ A_1 $, a másik két csúcsa pedig szintén a tizenkétszög valamelyik két csúcsával azonos? (Két háromszöget akkor tekintünk különbözőnek, ha legalább az egyik csúcsuk különböző.)

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Egy zöldségárus vállalkozó egyik reggel 200 kg első osztályú barackot visz eladásra a piacra. Tapasztalatból tudja, hogy az első osztályú barack eladási egységára és a napi eladott mennyiség között (jó közelítéssel) lineáris kapcsolat van (az eladott mennyiség az eladási egységár lineáris függvénye). Ha egész nap 500 Ft/kg áron kínálná a barackot, akkor várhatóan a fele fogyna el, míg ha 300 Ft/kg áron adná, akkor a 70%-a.

a) Mennyi lenne a zöldségárusnak az első osztályú barack eladásából származó bevétele, ha egész nap 400 Ft/kg-os egységáron kínálná a barackot?

b) Igazolja, hogy ha egész nap x (Ft/kg) az első osztályú barack egységára, y (kg) pedig a napi eladott mennyiség, akkor a közöttük lévő kapcsolat: $ y=-\dfrac{1}{5}x+200\ (0 < x < 1000) $.

A nap végén a 200 kg-ból megmaradó barackot a zöldségárus másnap már nem adhatja el első osztályúként. Ezért a megmaradó teljes mennyiséget eladja egy gyümölcsfeldolgozó vállalkozásnak, mégpedig 80 Ft/kg egységáron.

c) Mekkora eladási egységáron kínálja a barackot a zöldségárus napközben, hogy a napi bevétele maximális legyen? (A napi bevétel az első osztályúként eladott barackból származó bevétel plusz a gyümölcsfeldolgozó által fizetett összeg.)

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba