Egy nagy méretű, köztéren felállítandó óra számlapját szabályos 12-szög alakúra tervezik. Az $ A_1A_2\ldots A_{12} $ számlapot egy $ 260 cm \times 180 cm $-es téglalap alakú alumíniumlemezből vágják ki az ábra szerint.

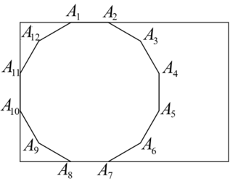
a) Mekkora tömegű az óralap, ha az alumíniumlemez vastagsága $ 2 mm $, és $ 1 m^3 $ alumínium tömege 2700 kg?

b) Jelöljük meg a szabályos tizenkétszög $ A_1 $ csúcsát! Hány olyan derékszögű háromszög van, amelynek egyik csúcsa az $ A_1 $, a másik két csúcsa pedig szintén a tizenkétszög valamelyik két csúcsával azonos? (Két háromszöget akkor tekintünk különbözőnek, ha legalább az egyik csúcsuk különböző.)

Megoldás:

a) $\approx 14\,kg$

b) $ 15 $