Legyen $ H $ azon $ r $ $ (0 < r < 1) $ racionális számok halmaza, amelyek végtelen periodikus tizedes tört alakja $ 0,abcabcabc . . . = 0,\dot{a}b\dot{c} $, ahol $ a $, $ b $, $ c $, nem feltétlenül különböző számjegyek. Felírva $ H $ elemeinek redukált tört alakját, hányféle számlálót kapunk?
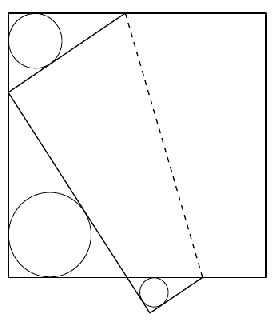
Egy négyzet alakú papírlapot úgy hajtunk meg, hogy a hajtásvonal a négyzet két szemköztes oldalát metssze, de ne menjen át a négyzet csúcsain. Ezután a keletkező háromszögekbe az alábbi ábra szerint egy-egy kört írunk. Bizonyítsuk be, hogy az így kapott három kör egyikének sugara megegyezik a másik két kör sugarának összegével!
A 900 számnak legfeljebb hány osztója választható ki úgy, hogy egyik se ossza egyik másikat se?


