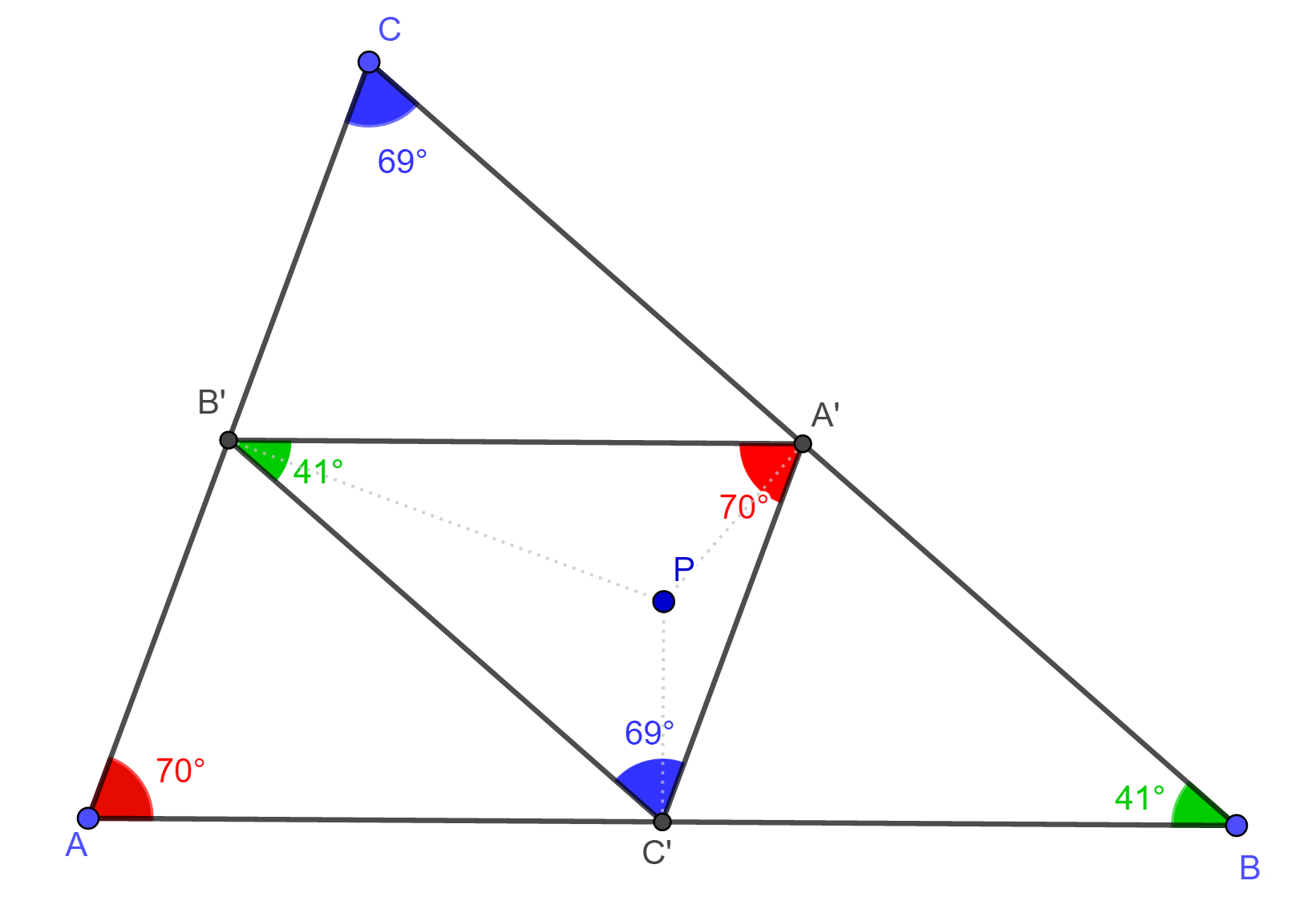
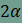| Szerkesztési feladatok |
| Területátalakítások |
| Szabályos sokszögek |
| Pitagorasz tétele |
| Tengelyes tükrözés |
| Középpontos tükrözés |
| Forgatás |
| Eltolás |
| Szélsőérték-feladatok (Markó Gábor munkája) |
Az
ABC
hegyesszögű
háromszög egy belső pontja P, a P pont BC,
BA és CA
oldalakra eső merőleges vetülete
rendre A’, C’
és B’. Határozzuk meg
az összes olyan P pontot, amelyre 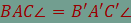 és és 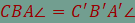 feltételek
teljesülnek! feltételek
teljesülnek! |
|
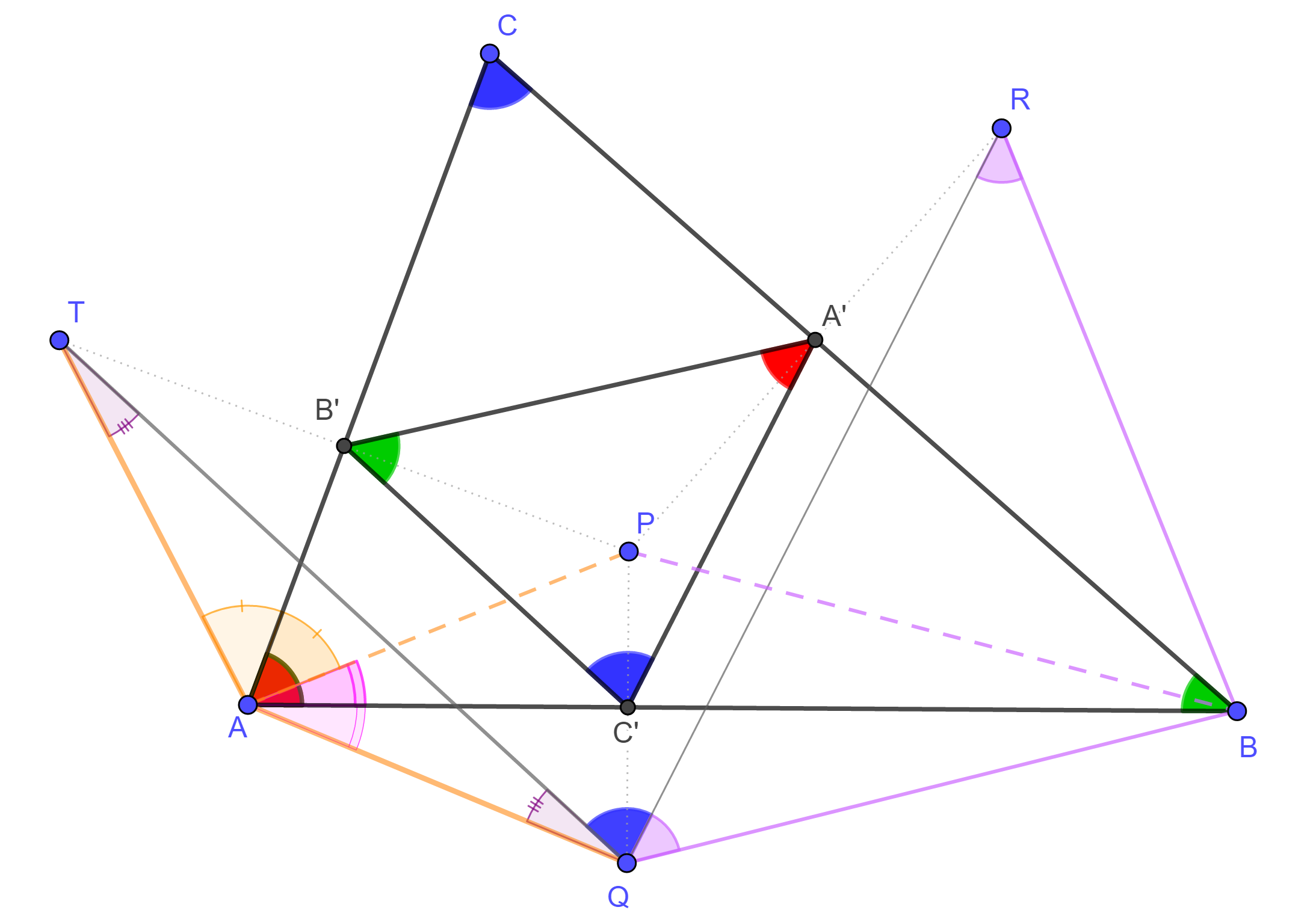
Az ABC háromszög szögeit a szokásos módon jelöljük. Tükrözzük az A’B’C’ háromszöget az AB, BC és CA oldalegyenesekre, a tükörképek legyenek rendre Q, R és T.
A
tükrözés miatt B’C’
középvonal a PTQ háromszögben,
ezért TQ párhuzamos B’C’-vel, és ugyanilyen
megfontolásból RQ párhuzamos A’C’-vel.
Ebből következik, hogy A QAT háromszög alapon fekvő szögeire
Gondolatmenetünk
az RQB háromszögben is
alkalmazható, így
azt kapjuk, hogy
Ez
azt jelenti, hogy a P
pont illeszkedik az AB szakasz Ugyanígy
belátható, hogy a P pont nemcsak az
AB szakasz,
hanem az ABC háromszög másik két
oldalához
tartozó megfelelő látókörívére is illeszkedik; P
rajta van a BC szakasz
|
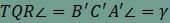
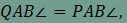
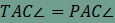
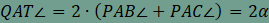 .
.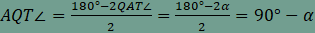
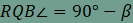
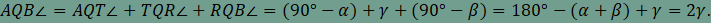
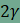
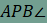
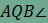
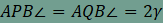 .
.