| Szerkesztési feladatok |
| Területátalakítások |
| Szabályos sokszögek |
| Pitagorasz tétele |
| Tengelyes tükrözés |
| Középpontos tükrözés |
| Forgatás |
| Eltolás |
| Szélsőérték-feladatok (Markó Gábor munkája) |
|
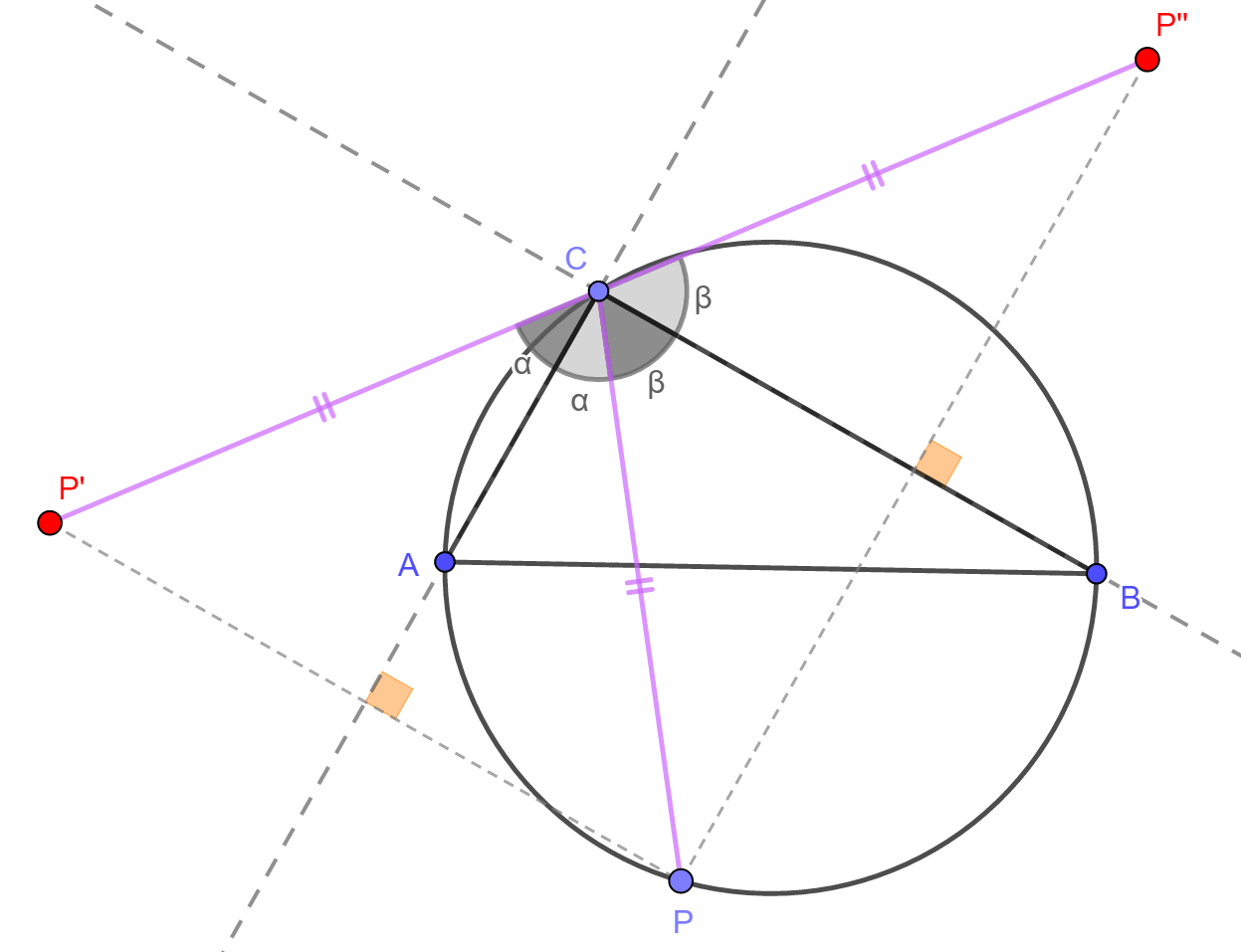
Az AB átmérőjű körvonal egyik félkörívén rögzítsünk egy A-tól és B-től különböző C pontot. A C pontot nem tartalmazó másik féköríven mozgó P pontot tükrözzük az AC illetve a BC egyenesre, a tükörképet jelölje rendre P' és P". Vizsgáljuk meg a P pont különböző helyzetei mellett a P', P" és C pontok kölcsönös helyzetét! Határozzuk meg, hogy mely P pont esetén lesz a P'CP" töröttvonal hossza a lehető legkisebb, illetve a lehető legnagyobb! Határozzuk meg a minimum és a maximum értékét! |
|
Az
animáció alapján azonnal látható, hogy a P', C és P'' pontok egy
egyenesre illeszkednek, továbbá C
felezi a P'P"
szakaszt. Ezt könnyen végiggondolhatjuk, ha a P ponttal együtt a CP
szakaszt is tükrözzük az AC
illetve BC
egyenesekre. A tükrözés szögtartó tulajdonsága alapján
A fentiek alapján a P'CP'' töröttvonal valójában egy szakasz, melynek hossza pont kétszerese a CP szakasz hosszának. Ezért P'P'' akkor a lehető legnagyobb, amikor CP is a lehető legnagyobb, azaz amikor CP átmérő a körben. Ebben az esetben a P'P" szakasz hossza a kör átmérőjének kétszerese. A P'P'' szakasz akkor a lehető legkisebb, amikor CP is a lehető legkisebb, ez pedig abban az esetben van, amikor P egybeesik az A vagy a B ponttal, attól függően, hogy az ABC háromszögnek melyik befogója a rövidebb. Ebben az esetben a P'P'' szakasz hossza az ABC háromszög rövidebb befogójának kétszerese. Összefoglalva: a P'P'' szakasz hossza az ABC derékszögű háromszög rövidebb befogójának kétszerese, valamint átfogójának kétszerese között változhat. |
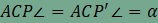 , és
, és 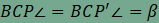 , ezért
, ezért 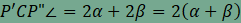 .
Thalész- tétele alapján azonban az
.
Thalész- tétele alapján azonban az 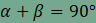 ,
amiből azonnal következik, hogy
,
amiből azonnal következik, hogy 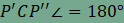 , és így a
, és így a 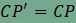 és
és 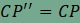 , ezért
, ezért