| Szerkesztési feladatok |
| Területátalakítások |
| Szabályos sokszögek |
| Pitagorasz tétele |
| Tengelyes tükrözés |
| Középpontos tükrözés |
| Forgatás |
| Eltolás |
| Szélsőérték-feladatok (Markó Gábor munkája) |
Markó Gábor, a Révai Miklós Gimnázium 10. osztályos tanulójának munkája Adott hegyesszögű háromszög belsejében van-e olyan pont, amelynek a háromszög csúcsaitól vett távolságösszege minimális? |
|
Ahogyan azt az
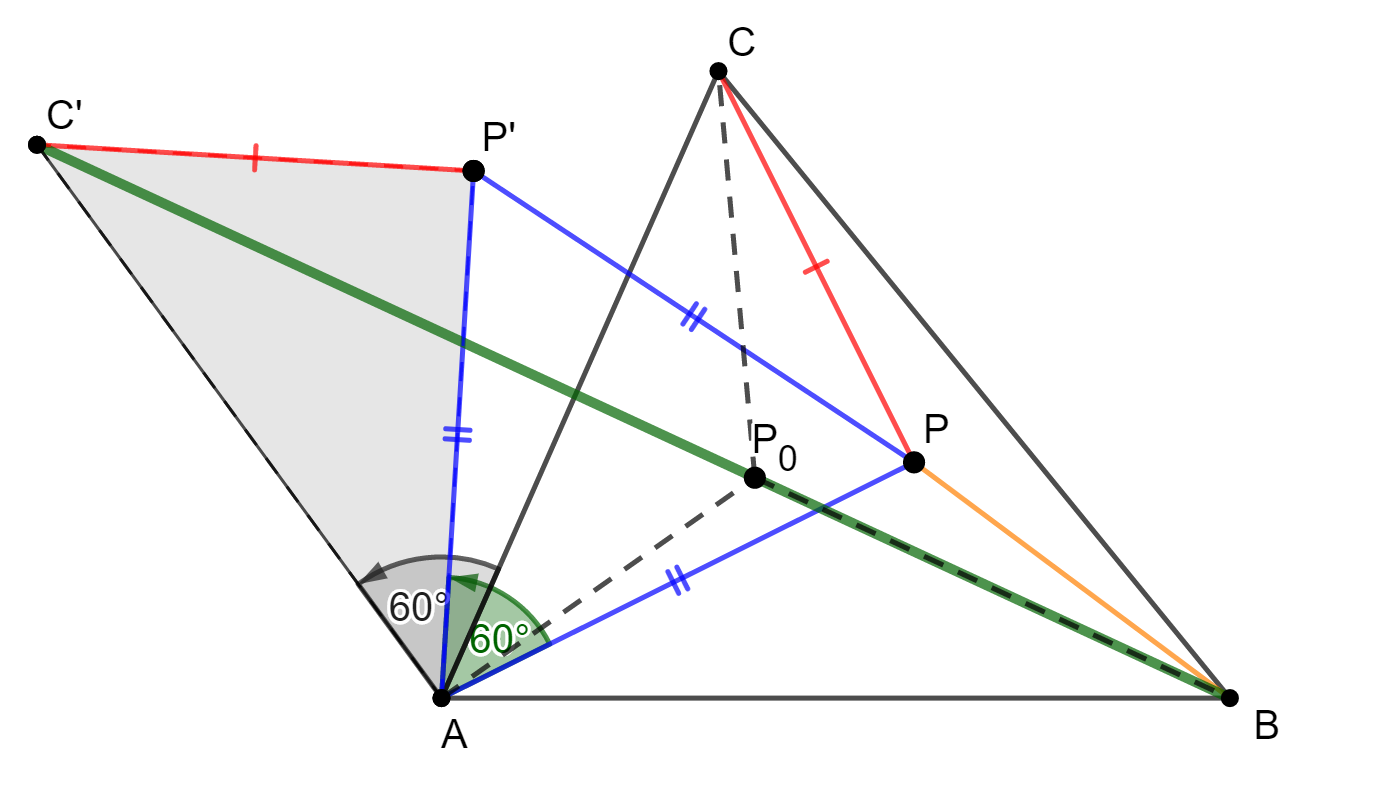
animáció is mutatja, forgassuk el az APC△-et az A
pont körül 60°-kal. Így az APC△ átkerül az AP’C’△
helyzetébe. A forgatás távolságtartása miatt az APP’△
egyenlő szárú, a szárszöge pedig PAP’∢ a forgatás
szögével egyenlő, azaz 60°. Ebből
következik, hogy az APP’△ szabályos,
tehát AP=PP’.
Szintén a távolságtartás miatt CP=C’P’,
ezért a P pont
csúcsoktól vett távolságösszegére AP+BP+CP
= BP+PP’+P’C’.
Így a BPP’C’ töröttvonal hossza az ABC△
P pontjának az A, B
és C csúcsoktól való
távolságának összege.
Tudjuk azonban, hogy a C’ pont helyzete a P helyzetétől teljesen független, ezért a BPP’C’ töröttvonal hosszának minimális értéke megegyezik a C’B szakasz hosszával, ugyanis két pont egyenesvonalú összeköttetése mindig a legrövidebb, ezt mutatja az animáció is. Ebből adódik, hogy a PA+PB+PC összeg minimuma éppen a C’B szakasz hosszával egyenlő, ez a minimum pedig úgy érhető el, ha a P és P’ pontok illeszkednek a C’B szakaszra. Legyen P pont minimális helyzete P0, amelynek helyzete pontosan meg van határozva, mert az AP0C’∢ 60°-os. Így az AP0C’∢ mellékszöge, azaz AP0B∢ 120°-os. A szerkesztésből az is látszik, hogy egyetlen ilyen minimumtulajdonságú pont van, tehát ha A pont helyett B vagy C pontból indulunk ki, a szerkesztés ugyanahhoz a P0 ponthoz vezet. Ebből az alábbi következtetésre juthatunk. Ez a P0 pont tehát olyan pont, amelyikből a háromszög mindegyik oldala 120°-os szög alatt látszik, valamint egy hegyesszögű háromszögnek a csúcsoktól vett távolságösszege ebben a pontban minimális. Az ilyen tulajdonságú pontot a háromszög izogonális vagy Fermat-féle pontjának nevezzük.
|