Menü
| Szerkesztési feladatok |
| Területátalakítások |
| Szabályos sokszögek |
| Pitagorasz tétele |
| Tengelyes tükrözés |
| Középpontos tükrözés |
| Forgatás |
| Eltolás |
| Szélsőérték-feladatok (Markó Gábor munkája) |
Markó Gábor, a Révai Miklós Gimnázium 10. osztályos tanulójának munkája Adott egy f egyenes, és ugyanazon az oldalán két pont, A és B. Az A pontból szeretnénk eljutni B-be a legrövidebb úton úgy, hogy közben érintsük az f egyenest. Melyik a legrövidebb út, hol kell érinteni az f egyenest? |
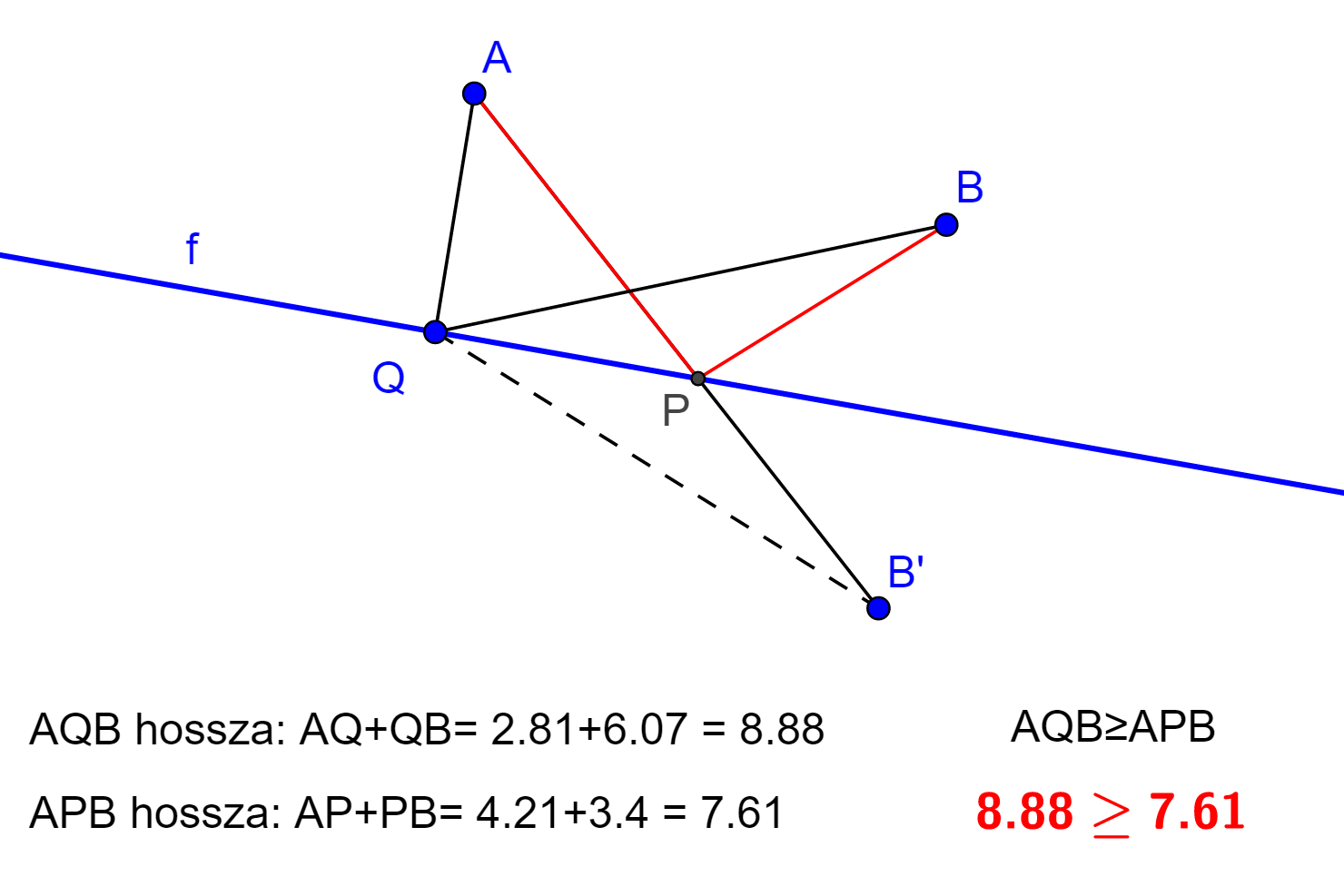
| A legrövidebb utat úgy kapjuk meg, hogy a B pontot tükrözzük az f egyenesre, majd a kapott B' tükörképet összekötjük az A ponttal. Így az AB’ szakasz kimetszi az f egyenesből a P pontot, amit érintve a legrövidebb úton juthatunk el A-ból B-be. A háromszög-egyenlőtlenség miatt ugyanis az f egyenes bármely más Q pontjára AQ+BQ=AQ+B’Q>B’A=AP+PB. Ahogyan az animáció is mutatja, az AQB út minden esetben hosszabb lesz, mint az APB út.
|