Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium
Látogatók
Összes: 6 574 026 Mai: 2 660
|
1. találat: OKTV 2014/2015 I. kategória 2. forduló 1. feladat
Témakör: *Algebra (egyenletrendszer) (Azonosító: OKTV_20142015_1k2f1f )
Adja meg az összes olyan $(x, y)$ valós számpárt, amely megoldása a következő egyenletrendszernek: $\begin {cases}\displaystyle x^{2}y+xy^{2}=6 \\\displaystyle \dfrac{1}{x}+\dfrac{1}{y}=\dfrac{3}{2}\end {cases}.$
*Geometria (kör, rombusz) (Azonosító: OKTV_20142015_1k2f2f )
Az $ABCD$ rombusz hegyesszöge $ 45^{\circ}$ . Mutassa meg, hogy a rombusz beírt körének tetszőleges $P$ pontjára teljesül $PA^{2}+PB^{2}+PC^{2}+PD^{2}=\dfrac{5}{2}AB^{2}.$
*Geometria (kör) (Azonosító: OKTV_20142015_1k2f3f )
Egy négyzetes oszlop alapélének és magasságának számértéke egész. A négyzetes oszlop $V$ térfogatának és $A$ felszínének mérőszámai között fennáll a $V=2015\cdot A$ összefüggés. Hány olyan, nem egybevágó négyzetes oszlop létezik, amely megfelel ezeknek a feltételeknek?
*Geometria (trigonometria, terület) (Azonosító: OKTV_20142015_1k2f4f )
Az $ABC$ háromszög szögei $CAB\angle =75^{\circ}$ és $ ABC\angle =60^{\circ}$ . Legyenek az $ABC$ háromszög magasságpontjának a $BC,\,CA$ és $AB$ oldalakra vonatkozó tükörképei rendre az $X, Y$ és $Z$ pontok. Közelítő értékek használata nélkül határozza meg az $XYZ$ és $ABC$ háromszögek területének arányát!
*Geometria (terület, algebra) (Azonosító: OKTV_20142015_1k2f5f )
Papírból $ 6$ darab $a$ cm oldalhosszúságú négyzetet vágtunk ki, majd azokból egy-egy $L$ -alakot raktunk le a $b$ cm oldalhosszúságú, négyzet alakú asztallap két szemközti csúcsánál az ábra szerint. (A hatoldalú $L$ -alak kettő oldala $ 2a$ , négy oldala pedig $a$ hosszúságú.) Így az asztallap két feketével jelölt része kétszer, a csíkozással jelölt része pedig egyszer fedett. A nem fedett részek területének összege, a kétszer fedett (fekete) részek területének összege és az egyszer fedett (csíkozott) részek területének összege cm $^{2}$ -ben mérve, ebben a sorrendben egy pozitív tagokból álló, monoton növő számtani sorozat egymást közvetlenül követő tagjai. (Az ábra nem méretarányos.) Határozza meg a $b$ és $a$ oldalak arányának pontos értékét! 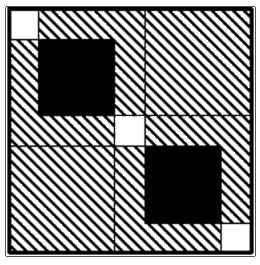
|
|
Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium
|
QR kód
Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium

|
|
Bejelentkezés cikkíróknak
|
|


