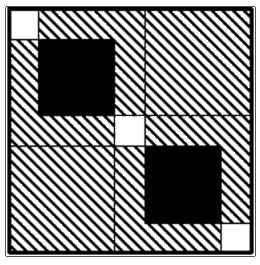
Papírból  $ 6$  darab  $a$  cm oldalhosszúságú négyzetet vágtunk ki, majd azokból egy-egy  $L$  -alakot raktunk le a  $b$  cm oldalhosszúságú, négyzet alakú asztallap két szemközti csúcsánál az ábra szerint. (A hatoldalú  $L$  -alak kettő oldala  $ 2a$  , négy oldala pedig  $a$  hosszúságú.) Így az asztallap két feketével jelölt része kétszer, a csíkozással jelölt része pedig egyszer fedett. A nem fedett részek területének összege, a kétszer fedett (fekete) részek területének összege és az egyszer fedett (csíkozott) részek területének összege cm  $^{2}$  -ben mérve, ebben a sorrendben egy pozitív tagokból álló, monoton növő számtani sorozat egymást közvetlenül követő tagjai. (Az ábra nem méretarányos.) Határozza meg a  $b$  és  $a$  oldalak arányának pontos értékét!

	Megnéz	Letölt
Megoldás