a) Oldja meg az alábbi egyenletet a valós számok halmazán!

$ (x-5)^2+7=2x $

b) Oldja meg az alábbi egyenletrendszert a valós számpárok halmazán!

$ \begin{cases} x+y=1 \\  0,7x+0,2y=x \end{cases} $

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Az ábrán látható diagram egy végzős évfolyam négy osztályában mutatja a fiúk és a lányok számát.

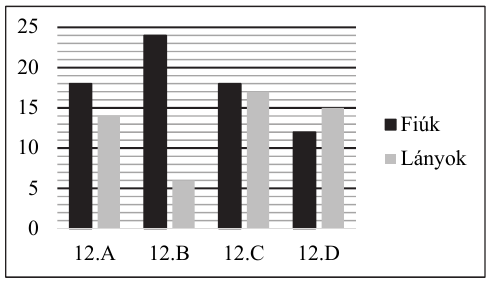a) A legkisebb létszámú osztályban a lányok száma hány százaléka a fiúk számának?

b) Töltse ki az alábbi táblázatot, majd határozza meg a 4 adat terjedelmét, átlagát és szórását!

A 12.B osztályban a lányok év végi matematikajegyeinek átlaga 4,5, az egész osztály matematikajegyeinek átlaga pedig 4,1 volt.
c) Mennyi volt a 12.B osztályban a fiúk átlaga matematikából év végén?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Bálint szőlőt termeszt a Balaton-felvidéken. A szőlő egy részéből $ 100\% $-os szőlőlevet készít. 1 liter szőlőlé 1,3 kg szőlő felhasználásával készül. Az elkészült szőlőlevet 5 literes műanyag tasakokba töltik.
a) Hány teli tasak szőlőlé készül 4,7 tonna szőlőből?
Az 5 literes tasakot téglatest alakú papírdobozba teszik. A doboz éleinek hossza 12 cm, 20 cm és 25 cm.
b) Hány literes a doboz?
Bálint telke téglalap alakú. A telek szomszédos oldalainak aránya 3 : 4, területe 1,47 hektár (1 hektár = 10 000 $ m^2 $).
c) Mekkora ennek a teleknek a kerülete?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Az új autók értéke a megvásárlás pillanatától kezdve csökken. A csökkenés mértékét különböző modellekkel lehet becsülni. A lineáris becslési módszer szerint az autó minden hónapban ugyanannyi forintot veszít az értékéből.
a) Egy újonnan 6 millió forintba kerülő autó értéke a lineáris becslési módszer szerint 5 év alatt csökken a felére. Hány forinttal csökken az autó értéke egy hónap alatt?
Az exponenciális modell szerint az új autó értéke havonta $ 1\% $-kal csökken.
b) Hány forintra csökken a 6 millió forintba kerülő új autó értéke két év alatt az exponenciális modell szerint, és ez hány százalékos csökkenést jelent az új kori értékéhez képest?
c) Hány hónap alatt csökken a felére az autó értéke az exponenciális modell szerint?
Egy autókereskedő a következő évre üzleti tervet készít. A terv szerint januárban 65 darab autót ad el, februártól kezdve pedig havonta egyre több autó eladásával számol: minden hónapban ugyanannyival növelné az értékesített autók számát az azt megelőző hónaphoz képest. Az éves terv szerint összesen 1110 darab autó eladása a cél.
d) Hány darabbal kell növelnie hónapról hónapra az eladást a terv szerint?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

A képen egy kerámia tárolóedény és a parafából készült teteje látható.

Az edény belseje egy csonkakúp alakú és egy ugyanolyan magasságú forgáshenger alakú részből áll. Az edény belső méretei: alapkörének átmérője 14 cm, a hengeres rész átmérője 11 cm, az edény teljes magassága 21 cm.
a) Számítsa ki az edény térfogatát!
A kerámiaedény belső felületét vékony zománcréteggel vonták be.
b) Számítsa ki, hogy egy edényen hány $ cm^2 $-es a zománcozott felület! 
Egy szállodában 20 db egyforma fedett edényben kétféle müzlikeveréket tartanak. 5 edényben natúr, 15 edényben csokis müzli van. Egy alkalmazott a reggeli sietségben véletlenszerűen választ ki az edények közül 4-et, és ezeket egy tálcára teszi.
c) Mekkora a valószínűsége annak, hogy a 4 edény közül egyben natúr, háromban pedig csokis müzli lesz?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

a) Határozza meg az alábbi állítások logikai értékét (igaz vagy hamis)! ($ A $ és $ B $ halmazokat jelöl. Válaszait itt nem kell indokolnia.)
I. állítás: Ha $ B $ üres halmaz, akkor $ A \cap B $ üres halmaz.
II. állítás: Ha $ A = B $, akkor $ A \setminus B $ üres halmaz.
III. állítás: $ Ha A \cup B = A $, akkor $ A = B $.

b) Az I. állítás megfordítása: Ha $ A \cap B $ üres halmaz, akkor $ B $ üres halmaz. Határozza meg ennek az állításnak a logikai értékét! Válaszát indokolja!

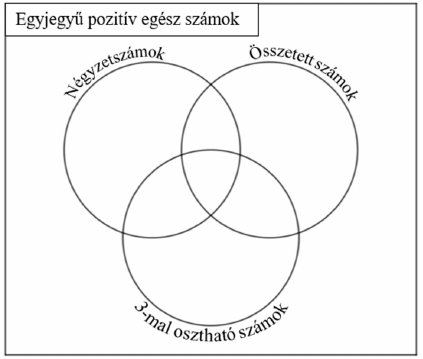
c) Írja be mind a kilenc egyjegyű pozitív egész számot az ábra megfelelő részébe!

A 0, 1, 2, 4 és 9 számjegyeket felhasználva elkészítjük az összes olyan ötjegyű számot, melyek különböző számjegyekből állnak.
d) Hány 4-gyel osztható szám van az elkészített számok között?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba