Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium
Látogatók
Összes:
7 327 765 Mai:
4 830 18-97-14-82.crawl.commoncrawl.org
(IP: 18.97.14.82) HonlapokSULINET Matematika Oktatási Hivatal Versenyvizsga portál Matematika Portálok |
1. találat: Matematika középszintű érettségi, 2022. május I. rész, 1. feladat Témakör: *Algebra (Azonosító: mmk_202205_1r01f ) Az $ A $ és $ B $ halmazokról tudjuk, hogy $ A = \{2; 3; 5\} $, $ A \cap B = \{2; 3\} $, $ A \cup B = \{1; 2; 3; 4; 5\} $. Elemei felsorolásával adja meg a $ B $\ halmazt! Témakör: *Kombinatorika (Azonosító: mmk_202205_1r02f ) 3. találat: Matematika középszintű érettségi, 2022. május I. rész, 3. feladat Témakör: *Algebra (Azonosító: mmk_202205_1r03f ) Melyik az a szám, amely 10-zel kisebb az ellentettjénél? Témakör: *Algebra (Azonosító: mmk_202205_1r04f ) Válassza ki az alábbiak közül a valós számok halmazán értelmezett $ x \rightarrow (x - 2)^2 $ függvény grafikonját!
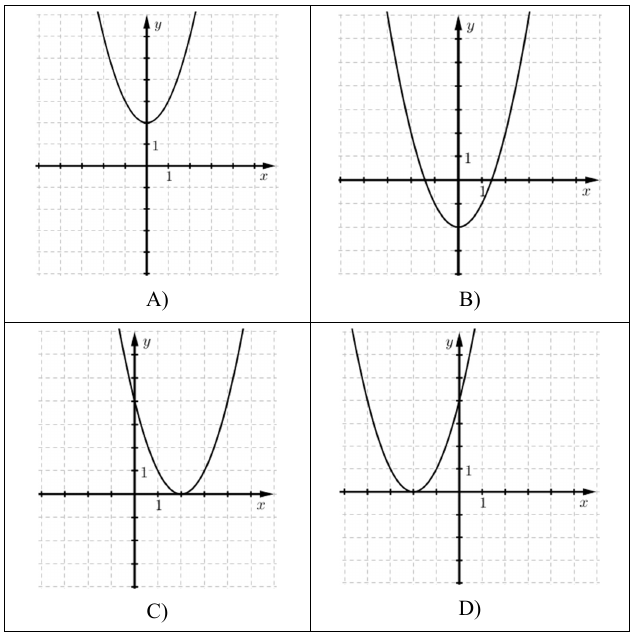
Témakör: *Geometria (Azonosító: mmk_202205_1r05f ) Egy derékszögű háromszög egyik befogója 5 cm hosszú, a háromszög ezzel szemközti szöge $ 32^\circ $-os. Számítsa ki a másik befogó hosszát! Megoldását részletezze! Témakör: *Kombinatorika (Azonosító: mmk_202205_1r06f ) Egy feleletválasztós teszt 5 kérdésből áll, minden kérdésnél négy válaszlehetőség van. Hányféleképpen lehet az 5 kérdésből álló tesztet kitölteni, ha minden kérdésnél egy választ kell megjelölni? Témakör: *Algebra (Azonosító: mmk_202205_1r07f ) Egy mértani sorozat második tagja $ 1,5 $, hányadosa $ 3 $. Számítsa ki a sorozat hatodik tagját és az első tíz tagjának az összegét! Megoldását részletezze! Témakör: *Algebra (Azonosító: mmk_202205_1r08f ) Számítsa ki az $ A(5; –3) $ és $ B(1; 0) $ pontok távolságát! Témakör: *Geometria (Azonosító: mmk_202205_1r09f ) Az ábrán látható kocka $ A $ csúcsából kiinduló élvektorai $ p $, $ q $ és $ r $. Fejezze ki $ p $, $ q $ és $ r $ segítségével a $ \overrightarrow{BH} $ vektort!
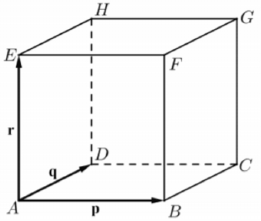
Témakör: *Algebra (Azonosító: mmk_202205_1r10f ) Adott a $ \left[–8; 4\right] $ zárt intervallumon értelmezett $ x \rightarrow \dfrac{1}{2}x + 3 $ függvény. Adja meg a függvény zérushelyét és értékkészletét! Témakör: *Kombinatorika (Azonosító: mmk_202205_1r11f ) 2021. október közepén közvéleménykutató szavazást indított a Budapesti Közlekedési Központ (BKK), melyben arra voltak kíváncsiak, hogy az utasok 30, 60 vagy 90 perces időalapú mobiljegyet szeretnének-e leginkább. A szavazásból kiderült, hogy a válaszadók fele 60 perces jegyet szeretne, 30 százalékuk választotta a 90 perceset, 20 százalékuk pedig a 30 perceset. Készítsen kördiagramot a szavazás eredményéről! Témakör: *Kombinatorika (Azonosító: mmk_202205_1r12f ) Feldobunk három szabályos pénzérmét. Határozza meg annak a valószínűségét, hogy a három pénzérmével azonosat dobunk (mindhárommal fejet, vagy mindhárommal írást)!
|
KeresésHonlapokKözépiskolai Matematikai és Fizikai Lapok Wolfram Alpha Art of Problem Solving Kvant IMO |
|||||||||||||||||
|
Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium
| |||||||||||||||||||
| |||||||||||||||||||
|
Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium
|
|
1082 Budapest, Horváth Mihály tér 8. OM azonosító: 035277 |
Joomla template: szsnjm4-001 (c) Szoldatics József 2011/2024
www.szolda.hu
www.szolda.hu