Oldja meg az alábbi egyenleteket a valós számok halmazán!

a) $\dfrac{2}{x-2}=x-3$

b) $ 9^{x+1}-7 \cdot 9^x =54$

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Andrea és Gabi közösen, de különböző edzésmódszerrel készülnek egy futóversenyre. A felkészülés első hetében mindketten 15 km-t, a felkészülés tizenegyedik (11.) hetében pedig már mindketten 60 km-t futnak.

Andrea hétről hétre ugyanannyi kilométerrel növeli a lefutott táv hosszát.

a) Hány kilométerrel fut többet hétről hétre Andrea?

b) Hány kilométert fut Andrea a 11 hét alatt összesen?

Gabi hétről hétre ugyanannyi százalékkal növeli a lefutott táv hosszát.

c) Hány százalékkal fut többet hétről hétre Gabi?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Az ABCD rombusz AC átlójának hossza 12 cm, BD átlójának hossza 5 cm.

a) Számítsa ki a rombusz belső szögeinek nagyságát!

A rombuszt megforgatjuk az AC átló egyenese körül.

b) Számítsa ki az így keletkező forgástest felszínét!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

A 2016-os nyári olimpián a magyar sportolók 8 arany, 3 ezüst és 4 bronzérmet szereztek.

a) Készítsen kördiagramot, amely az érmek eloszlását szemlélteti!

Egy 32 fős osztályban kétszer annyian nézték 2016 nyarán a női kajak négyesek olimpiai döntőjét, mint a labdarúgó Európa-bajnokság döntőjét. 10 diák mindkét sportesemény közvetítését nézte.

b) Hányan nézték az osztályból csak a női kajak négyesek olimpiai döntőjét, ha mindenki nézte legalább az egyik sporteseményt?

Egy iskolai vetélkedőn az alábbi szelvényen kell eltalálni a 2016-os nyári olimpia női kajak négyes számában az első hat helyezett nemzet sorrendjét. Péter azt tudja, hogy holtverseny nem volt, a magyarok lettek az elsők, a többi helyezettre viszont egyáltalán nem emlékszik.

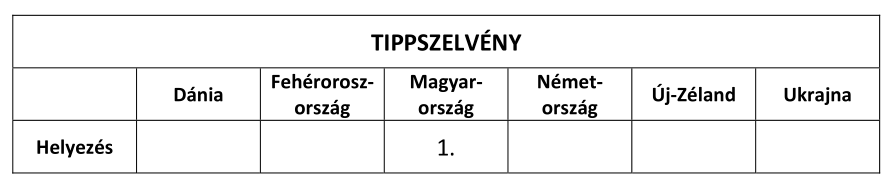
Péter az üres mezőkbe beírja a tippjét: valamilyen sorrendben a 2, 3, 4, 5, 6 számokat.

c) Számítsa ki annak a valószínűségét, hogy Péter – a magyarokon kívül – még legalább három nemzet helyezését eltalálja!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Adott az $x+2y=13$ egyenletű e egyenes és az $x^2+(y+1)^2-45=0$ egyenletű k kör.

a) Adja meg az e egyenes meredekségét, és azt a pontot, ahol az egyenes metszi az y tengelyt!

b) Határozza meg a k kör középpontját és sugarának hosszát!

c) Számítással igazolja, hogy az e egyenesnek és a k körnek egyetlen közös pontja van!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Szabó tanár úrnak ebben az évben összesen 11 darab középszintű matematika érettségi dolgozatot kell kijavítania. Az először kijavított kilenc dolgozat pontszáma: 35, 40, 51, 55, 62, 67, 72, 84, 92.

a) Számítsa ki a kilenc dolgozat pontszámának átlagát és szórását!

Szabó tanár úr a javítás után a kilenc dolgozat közül három tanuló dolgozatát véletlenszerűen kiválasztja.

b) Számítsa ki annak a valószínűségét, hogy a három kiválasztott dolgozat közül legalább kettőnek a pontszáma legalább 60 pont!

Az utolsó két dolgozat kijavítása után Szabó tanár úr megállapítja, hogy a 11 dolgozat pontszámának mediánja 64, átlaga 65 pont lett.

c) Határozza meg az utoljára kijavított két dolgozat pontszámát!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba