Egy közvélemény-kutató intézet azt a feladatot kapta, hogy két alkalommal – fél év különbséggel – mérje fel a TV-ben látható három filmsorozat nézettségi adatait.

Az ábrán látható kérdőíven a válaszoló vagy azt jelölhette be, hogy az A, B és C sorozatok közül melyiket nézi (akár többet is meg lehetett jelölni), vagy azt, hogy egyiket sem nézi.

Az első felméréskor kapott 600 kérdőív jelöléseit összesítve megállapították, hogy az A sorozat összesen 90 jelölést kapott, a B sorozat összesen 290-et, a C sorozat pedig összesen 230-at. Érdekes módon olyan válaszadó nem volt, aki pontosan két sorozatot nézett volna, viszont 55-en mindhárom sorozatot bejelölték.

a) A válaszolók hány százaléka nézte az A sorozatot?

b) Hány válaszoló nem nézte egyik sorozatot sem?

A második felmérés után kiválogatták azokat a kérdőíveket, amelyeken valamelyik sorozat meg volt jelölve. Ezeken a három sorozat nézettségére összesen 576 jelölés érkezett. Az adatok feldolgozói minden jelölést megszámoltak, és a végeredményről az itt látható kördiagramot készítették. A második felmérés után kiválogatták azokat a kérdőíveket, amelyeken valamelyik sorozat meg volt jelölve. Ezeken a három sorozat nézettségére összesen 576 jelölés érkezett. Az adatok feldolgozói minden jelölést megszámoltak, és a végeredményről az itt látható kördiagramot készítették.

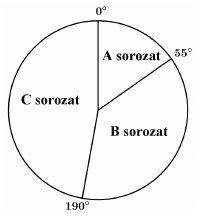
c) Számítsa ki, hogy az egyes sorozatok nézettségére hány jelölés érkezett!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Egy család személyautóval Budapestről Keszthelyre utazott. Útközben lakott területen belül, országúton és autópályán is haladtak. Az utazással és az autóval kapcsolatos adatokat a következő táblázat tartalmazza:

a) Mennyi ideig tartott az utazás?

b) Hány liter ezen az utazáson az autó 100 km-re eső átlagfogyasztása? Válaszát egy tizedesjegyre kerekítve adja meg!

Útközben elfogyott az autóból a benzin. A legközelebbi benzinkútnál kétféle benzineskannát lehet kapni. A nagyobbra rá van írva, hogy 20 literes, a kisebbre nincs ráírva semmi. A két kanna (matematikai értelemben) hasonló, a nagyobb kanna magassága éppen kétszerese a kisebb kanna magasságának.

c) Hány literes a kisebb kanna?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Egy téglatest alakú akvárium egy csúcsból kiinduló élei 30 cm, 40 cm, illetve 50 cm hosszúak.

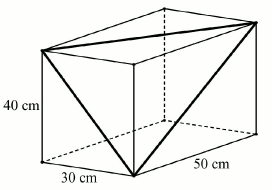
a) Hány literes ez az akvárium? (A számolás során tekintsen el az oldallapok vastagságától!)

Tekintsük azt a háromszöget, amelynek oldalait az ábrán látható téglatest három különböző hosszúságú lapátlója alkotja.

b) Mekkora ennek a háromszögnek a legkisebb szöge? Válaszát fokban, egészre kerekítve adja meg!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Egy számtani sorozat első tagja 56, differenciája –4.
a) Adja meg a sorozat első 25 tagjának összegét!
b) Számítsa ki az n értékét és a sorozat n-edik tagját, ha az első n tag összege 408.
Egy mértani sorozat első tagja 10²⁵, hányadosa 0,01.
c) Hányadik tagja ennek a sorozatnak a 100 000?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

A biliárdjáték megkezdésekor az asztalon 15 darab azonos méretű, különböző színezésű biliárdgolyót helyezünk el háromszög alakban úgy, hogy az első sorban 5 golyó legyen, a másodikban 4, a következőkben pedig 3, 2, illetve 1 golyó. (A golyók elhelyezésére vonatkozó egyéb szabályoktól tekintsünk el.)

a) Hányféleképpen lehet kiválasztani a 15-ből azt az 5 golyót, amelyet majd az első sorban helyezünk el? (Az 5 golyó sorrendjét nem vesszük figyelembe.)

b) Hányféle különböző módon lehet az első két sort kirakni, ha a 9 golyó sorrendjét is figyelembe vesszük?

Egy biliárdasztal játékterülete téglalap alakú, mérete 194 cm × 97 cm. A játékterület középpontja felett 85 cm-rel egy olyan (pontszerűnek tekinthető) lámpa van, amely fénykúpjának a nyílásszöge 100°.

c) Számítással állapítsa meg, hogy a lámpa megvilágítja-e a játékterület minden pontját!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Egy focicsapat 11 játékosa megérkezik az edzésre, néhányan kezet fognak egymással. (Két játékos között legfeljebb egy kézfogás történik.) Az edző felírta, hogy ki hányszor fogott kezet, és a következő számokat kapta: 0; 1; 2; 2; 2; 5; 0; 0; 4; 4; 2.

a) Ábrázolja a kézfogásoknak egy lehetséges gráfját, ahol a pontok a játékosokat jelölik, és két pont között akkor van él, ha az illetők kezet fogtak az edzés előtt!

b) Hány kézfogás történt összesen?

Egy másik alkalommal az edző által feljegyzett 11 nemnegatív egész számról a következőket állapítottuk meg: a számok egyetlen módusza 2, mediánja 3, átlaga 4, terjedelme pedig 5 volt.

c) Adjon meg a fenti feltételeknek megfelelő 11 nemnegatív egész számot!

Az edzésen a játékosok a tizenegyesrúgást gyakorolják. Az egyik játékos 0,9 valószínűséggel lövi be a tizenegyest.

d) Mennyi a valószínűsége annak, hogy három rúgásból legalább egyszer betalál? A valószínűség pontos értékét adja meg!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba